题目内容
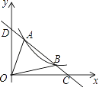
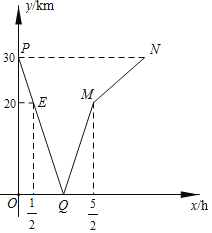
【题目】甲、乙两人分别从A，B两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到达B地后，乙继续前行．设出发xh后，两人相距ykm，图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系．
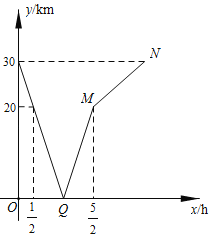
（1）根据图中信息，求出点Q的坐标，并说明它的实际意义；
（2）求甲、乙两人的速度．
【答案】（1）Q（1.5，0），意义：甲、乙两人分别从A，B两地同时出发后，经过1.5小时两人相遇；（2）甲、乙的速度分别为12km/h、8km/h
【解析】
（1）根据待定系数法，求出直线PQ解析式，从而求出点Q得坐标，再说出它的实际意义，即可；
（2）设甲的速度为akm/h，乙的速度为bkm/h，根据图象列出二元一次方程组，即可求解．
（1）设直线PQ解析式为：y＝kx+b，
把已知点P(0，30)，E(
，20)代入得:
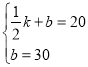，解得：
，
∴直线PQ解析式为：y＝﹣20x+30，
∴当y＝0时，x＝1.5，
∴Q(1.5，0)．
它的实际意义是：甲、乙两人分别从A，B两地同时出发后，经过1.5小时两人相遇；
（2）设甲的速度为akm/h，乙的速度为bkm/h，
由第（1）题得，甲、乙经过1.5小时两人相遇；由图象得：第
h时，甲到B地，
∴
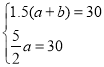，解得：
．
答：甲、乙的速度分别为12km/h、8km/h．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
