题目内容
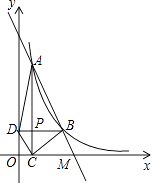
【题目】已知：如图，在边长为1的小正方形网格中，△ABC的顶点都在格点上，建立适当的平面直角坐标系xOy，使得点A、B的坐标分别为（2，3）、（3，2）．
（1）在网格中画出满足要求的平面直角坐标系，写出点C的坐标为 ；
（2）若点P是x轴上的一个动点，则PA+PB的最小值为 ．（直接写出结果）
【答案】（1）（1，0）（2）
【解析】
（1）根据A、B两点坐标，确定平面直角坐标系即可；
（2）作当C关于y轴的对称点C′，连接AC′交y轴于P，此时PA+PC的值最小，最小值=AC′；
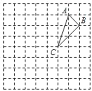
解：（1）平面直角坐标系的画法如下图所示：
点C的坐标为（1，0）；
（2）作当B关于x轴的对称点B′，连接AB′交x轴于P，此时PA+PB的值最小，最小值=AB′=
=．
练习册系列答案
相关题目
