题目内容
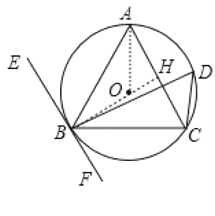
【题目】如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=![]() cm.
cm.
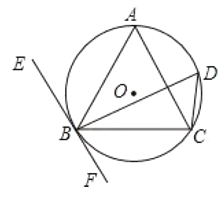
(1)请探究EF与⊙O的位置关系,并说明理由;
(2)求⊙O的周长.
【答案】(1)EF与⊙O相切.理由见解析;(2)⊙O的周长为2πcm.
【解析】
(1)延长BO交AC于H,如图,先证明△ABC为等边三角形,利用点O为△ABC的外心得到BH⊥AC,由于AC∥EF,所以BH⊥EF,于是根据切线的判定定理即可得到EF为⊙O的切线;
(2)连结OA,如图,根据等边三角形的性质得∠OAH=30°,AH=CH=![]() AC=
AC=![]() ,再在Rt△AOH中,利用三角函数和计算出OA=1,然后根据圆的周长公式计算.
,再在Rt△AOH中,利用三角函数和计算出OA=1,然后根据圆的周长公式计算.
(1)EF与⊙O相切.理由如下:
延长BO交AC于H,如图,
∵∠BAC=∠BDC=60°,
而∠ACB=60°,
∴△ABC为等边三角形,
∵点O为△ABC的外心,
∴BH⊥AC,
∵AC∥EF,
∴BH⊥EF,
∴EF为⊙O的切线;
(2)连结OA,如图,
∵△ABC为等边三角形,
∴OA平分∠ABC,
∴∠OAH=30°,
∵OH⊥AC,
∴AH=CH=![]() AC=
AC=![]() ,
,
在Rt△AOH中,∵cos∠OAH=![]() ,
,
∴OA=![]() =1,
=1,
∴⊙O的周长=2π×1=2π(cm).

练习册系列答案
相关题目