题目内容
已知y1＝x2－2x－3，y2＝x＋7，能使y1＝y2成立的x的取值为 ▲ ．
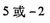
首先根据题意得到方程x2-2x-3=x+7，然后移项合并同类项，再把方程的左边分解因式，即可解出方程的解．
解：∵y1=y2，
∴x2-2x-3=x+7，
x2-2x-3-x-7=0，
x2-3x-10=0，
∴（x-5）（x+2）=0，
x1=5，x2=-2．
故答案为：5或-2．
此题主要考查了因式分解法解一元二次方程，关键是熟练掌握因式分解法解一元二次方程的一般步骤：①移项，使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零，得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解．
解：∵y1=y2，
∴x2-2x-3=x+7，
x2-2x-3-x-7=0，
x2-3x-10=0，
∴（x-5）（x+2）=0，
x1=5，x2=-2．
故答案为：5或-2．
此题主要考查了因式分解法解一元二次方程，关键是熟练掌握因式分解法解一元二次方程的一般步骤：①移项，使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零，得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解．
练习册系列答案
相关题目
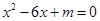有两个同号不相等的实数根，则m的取值范围是（ ）.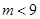
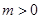
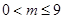
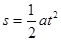。若飞机在起飞前滑行4000米的距离，其中a=20米/秒2 ，则飞机起飞用的时间t= 秒。
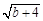＝0，求方程ax＋
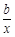＝7的解．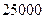
元的均价对外销售，由于国务院有关房地产的新政策出台，购房者持币观望．为了加快资金周转，房地产开发商对价格进行两次下调，最终以每平方米
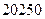元的均价开盘销售．
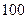平方米的房子．开发商还给予以下两种优惠方案以供选择：①一次付清全款打九九折；②一次付清全款不打折，送五年物业管理费．如该楼盘物业管理费是每月
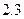元/米2．请问哪种方案更优惠？