题目内容
边长为整数的直角三角形,若其两直角边边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定直角三角形三边之长。(10分)
设直角边为a,b(a<b),则a+b=k+2,ab=4k,因为方程的根为整数,故△=(k+2)2-16k为完全平方数。
设(k+2)2-16k=n2 ∴k2-12k+4=n2 ∴(k-6)2-n2=32
∴(k+n-6)(k-n-6)=1×32=2×16=4×8
∵k+n-6>k-n-6 ∴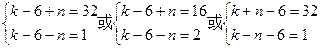
解得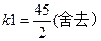 ,k2=15,k3=12
,k2=15,k3=12
当k2=15时,a+b="17,ab=60 " ∴a="15" , b="12 " , c=13;当k=12时,a+b=14,ab=48
∴a="6" , b="8 " ,c=10
设(k+2)2-16k=n2 ∴k2-12k+4=n2 ∴(k-6)2-n2=32
∴(k+n-6)(k-n-6)=1×32=2×16=4×8
∵k+n-6>k-n-6 ∴
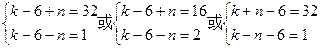
解得
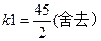 ,k2=15,k3=12
,k2=15,k3=12当k2=15时,a+b="17,ab=60 " ∴a="15" , b="12 " , c=13;当k=12时,a+b=14,ab=48
∴a="6" , b="8 " ,c=10
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
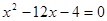 (2)
(2)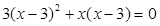 .
. ,
,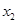 是一元二次方程
是一元二次方程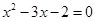 的两个实数根,则
的两个实数根,则 .
.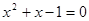 ,那么代数式
,那么代数式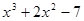 的值是( )
的值是( )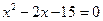 (2)
(2)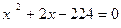 (用配方法解)
(用配方法解)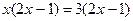 (4)
(4)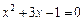
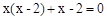
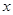 的方程
的方程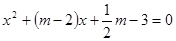 .
.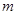 取什么实数,这个方程总有两个不相等的实数根;
取什么实数,这个方程总有两个不相等的实数根;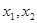 满足
满足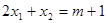 ,求
,求