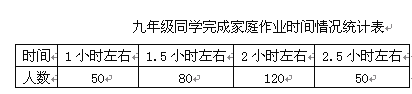
题目内容
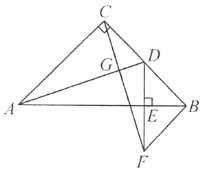
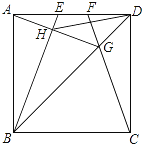
【题目】如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论正确的个数是( )
①△ABG∽△FDG ②HD平分∠EHG ③AG⊥BE ④S△HDG:S△HBG=tan∠DAG ⑤线段DH的最小值是2 ![]() ﹣2.
﹣2.
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
解:∵四边形ABCD是正方形,∴AB=CD,∠BAD=∠ADC=90°,∠ADB=∠CDB=45°.在△ABE和△DCF中,∵AB=CD,∠BAD=∠ADC,AE=DF,∴△ABE≌△DCF(SAS),∴∠ABE=∠DCF.在△ADG和△CDG中,∵AD=CD,∠ADB=∠CDB,DG=DG,∴△ADG≌△CDG(SAS),∴∠DAG=∠DCF,∴∠ABE=∠DAG.∵∠DAG+∠BAH=90°,∴∠ABE+∠BAH=90°,∴∠AHB=90°,∴AG⊥BE,故③正确.
同法可证:△AGB≌△CGB.∵DF∥CB,∴△CBG∽△FDG,∴△ABG∽△FDG,故①正确.
∵S△HDG:S△HBG=DG:BG=DF:BC=DF:CD=tan∠FCD.又∵∠DAG=∠FCD,∴S△HDG:S△HBG=tan∠FCD,tan∠DAG,故④正确.
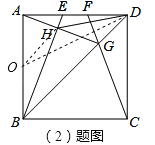
取AB的中点O,连接OD、OH,∵正方形的边长为4,∴AO=OH=![]() ×4=2,由勾股定理得,OD=
×4=2,由勾股定理得,OD=![]() =
=![]() ,由三角形的三边关系得,O、D、H三点共线时,DH最小,DH最小=
,由三角形的三边关系得,O、D、H三点共线时,DH最小,DH最小=![]() .故⑤正确.
.故⑤正确.
无法证明DH平分∠EHG,故②错误,故①③④⑤正确,故选C.

练习册系列答案
相关题目