Question

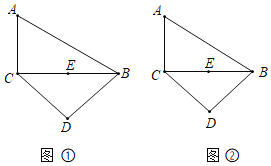
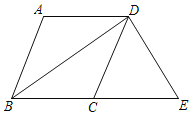
【题目】如图，面积为24的ABCD中，对角线BD平分∠ABC，过点D作DE⊥BD交BC的延长线于点E，DE＝6，则sin∠DCE的值为（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

连接AC，过点D作DF⊥BE于点E，由BD平分∠ABC证得四边形ABCD是菱形，利用DE⊥BD得到OC∥ED求出AC，根据ABCD面积为24求出BD，再由勾股定理求出BC，设CF＝x，则BF＝5+x，利用BD2﹣BF2＝DC2﹣CF2求出x得到DF，即可求出答案.

解：连接AC，过点D作DF⊥BE于点E，

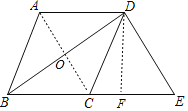
∵BD平分∠ABC，

∴∠ABD＝∠DBC，

∵ABCD中，AD∥BC，

∴∠ADB＝∠DBC，

∴∠ADB＝∠ABD，

∴AB＝BC，

∴四边形ABCD是菱形，

∴AC⊥BD，OB＝OD，

∵DE⊥BD，

∴OC∥ED，

∵DE＝6，

∴OC＝，

∴AC=6，

∵ABCD的面积为24，

∴，

∴BD＝8，

∴＝＝5，

设CF＝x，则BF＝5+x，

由BD2﹣BF2＝DC2﹣CF2可得：82﹣（5+x）2＝52﹣x2，

解得x＝，

∴DF＝，

∴sin∠DCE＝．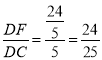

故选：A．