Question

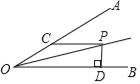
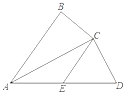
【题目】如图，在四边形ABCD中，∠B＝90°，对角线AC平分∠BAD，AC2＝ABAD．

（1）求证：AC⊥CD；

（2）若点E是AD的中点，连接CE，∠AEC＝134°，求∠BCD的度数．

Answer 1

【答案】(1)证明见解析；（2）157°．

【解析】

（1）易证△BAC∽△CAD，得∠B＝∠ACD＝90°，故可证明；（2）根据相似三角形的性质得∠ACB＝∠D＝67°，故可求出∠BCD.

（1）证明：∵AC2＝ABAD，

∴，

∵AC平分∠BAD，

∴∠BAC＝∠CAD，

∴△BAC∽△CAD，

∴∠B＝∠ACD＝90°，

∴AC⊥CD．

（2）∵∠ACD＝90°，AE＝ED，

∴EC＝EA＝ED，

∴∠D＝∠ECD，

∵∠AEC＝∠D+∠ECD＝134°，

∴∠ECD＝∠D＝67°，

∵△ABC∽△ACD，

∴∠ACB＝∠D＝67°，

∴∠BCD＝67°+90°＝157°．