题目内容
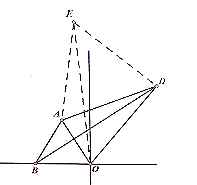
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,边
是等边三角形,边![]() 上有一点
上有一点![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.

(1)求![]() 的坐标(用含有
的坐标(用含有![]() 的式子表示);
的式子表示);
(2)如图(1),若点![]() 在线段
在线段![]() 上运动,点
上运动,点![]() 在
在![]() 轴的正半轴上运动.当
轴的正半轴上运动.当![]() 的值最小时,
的值最小时,![]() .
.
问:![]() 的面积是否为定值,若是,求其值;若不是,请说明理由.
的面积是否为定值,若是,求其值;若不是,请说明理由.
(3)如图(2),若在![]() 外还有一点
外还有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)(m-6,0);(2)是定值为25![]() ,理由见解析(3)12
,理由见解析(3)12
【解析】
(1)根据![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() ,即可写出
,即可写出![]() 的坐标;
的坐标;
(2)作出点E关于y轴的对称点E’,得到PE=PE’,E’为定点,P、F为动点,过E’作E’F⊥AB,交y轴于点P,此时PE+PF=E’F,E’F为点E’到AB的距离,为最小,若BF=7,△BFE’为直角三角形,根据∠B=60°得到BE’=14,EE’=8,OE=4,OB=10,即可求解△ABO的面积;
(3)将△ABD旋转60°到△AOE,得到OE=BD=15,△AED为等边三角形,得到DE=AD=9,∠ADE=60°,再得到∠EDO=90°,利用勾股定理即可求解.
(1)∵![]() ,且
,且![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() ,
,
∴![]() 的坐标为(m-6,0);
的坐标为(m-6,0);
(2)作出点E关于y轴的对称点E’,
∴PE=PE’,
∵E(m,0)
∴E’为定点,P、F为动点,过E’作E’F⊥AB,交y轴于点P,此时PE+PF=E’F,
E’F为点E’到AB的距离,为最小,
若BF=7,△BFE’为直角三角形,
∵∠B=60°∴∠BE’F=30°,
∴BE’=14,
∵BE=6
∴EE’=8,
∴OE=4,
则OB=10,
∴S△ABO=![]() =
=![]() =25
=25![]() ;
;

(3)将△ABD旋转60°到△AOE,
∴△ABD≌△AOE,
∴OE=BD=15,
∵AD=AE,∠EAD=60°,
∴△AED为等边三角形,得到DE=AD=9,∠ADE=60°,
∵![]()
∴∠EDO=∠ADE +∠ADO= 90°,
∴OD=![]()