题目内容
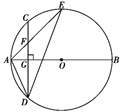
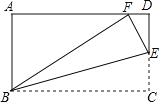
【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.

(1)证明:DC∥AB;
(2)求∠PFH的度数.
【答案】(1)见解析;(2)26°.
【解析】
(1)由DC∥FP知∠3=∠2,结合∠2=∠1,可得DC∥AB;
(2)利用平行线的判定得到AB∥PF∥CD,根据平行线的性质得到∠AGF=∠GFP,∠DEF=∠EFP,根据角平分线的定义求出∠GFH,即可求出∠PFH的度数.
解:(1)∵DC∥FP,
∴∠3=∠2,
又∵∠1=∠2,
∴∠3=∠1,
∴DC∥AB;
(2)∵DC∥FP,DC∥AB,∠FED=28°,
∴∠FED=∠EFP=28°,AB∥FP,
又∵∠AGF=80°,
∴∠AGF=∠GFP=80°,
∴∠GFE=∠GFP+∠EFP=80°+28°=108°,
又∵FH平分∠EFG,
∴∠GFH=![]() ∠GFE=54°,
∠GFE=54°,
∴∠PFH=∠GFP∠GFH=80°54°=26°.

练习册系列答案
相关题目
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.