Question

【题目】如图，D是等边△ABC的边BC的中点，E、F分别在AB、AC上，∠EDF+∠A=180°，AE:EB=5:1，EF=，则CF长为__________．

Answer 1

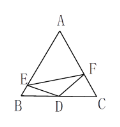
【答案】4

【解析】

取AB的中点M，连接DM，过点E作EN⊥AC，利用三角形中位线定理及AAS定理证得△DEM≌△DFC，从而得到EM=FC，然后设EB=x，结合等边三角形和含30°的直角三角形的性质求得AN=，EN=，NF=，然后利用勾股定理列方程求解，从而求出CF的长度．

解：取AB的中点M，连接DM

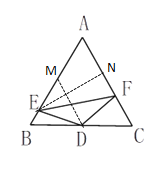
∵∠EDF+∠A=180°

∴在四边形AEDF中，∠AED+∠AFD=180°

又因为∠AFD+∠CFD=180°

∴∠AED=∠CFD

∵D是等边△ABC的边BC的中点，M为AB中点

∴DM∥AC，DM=，DC，AB=AC=BC

∴∠DMB=∠A=∠C=60°，DM=DC

∴△DEM≌△DFC

∴EM=FC

∵AE：EB=5：1

∴设EB=x，则AE=5x，AB=AC=6x

∴BM=3x，EM=FC=2x，AF=4x

过点E作EN⊥AC

在Rt△AEN中，∠AEN=30°

∴AN=，则EN=，NF=

∴在Rt△ENF中，

解得：x=±1（负值舍去）

∴CF=4

故答案为：4