��Ŀ����
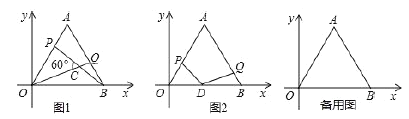
����Ŀ����������ͼ���������� ABCD �У�P �� CD ��һ���㣨�� C��D ���غ�����ʹ���ǰ��ֱ�Ƕ������ P �غϣ�����һ��ֱ�DZ�ʼ�վ����� B����һֱ�DZ��������ε�ijһ������ֱ�߽��ڵ� E��
��1�����ݲ����������������������ͼ�Σ�
��2���۲�����ͼ�Σ�д��һ�����BPC ���Ƶ������Σ���˵�����ɣ�
��3������ P λ�� CD ���е�ʱ��ֱ��д����2�����������������ε����Ʊȣ�
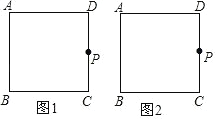
���𰸡���1����ͼ��ʾ����������2�����ۣ���PBC�ס�EPD�����ɼ���������3�����Ʊȣ�2��1��
��������
��1������Ҫ��ͼ�μ��ɣ� (2)���ۣ���PBC�ס�EPD���������Ƕ�Ӧ��ȵ��������������Ƽ���֤���� (3) �������������ε����ʼ��ɽ������.
��1����ͼ��ʾ��

��2�����ۣ���PBC�ס�EPD��
���ɣ����ı��� ABCD �������Σ�
���D����C��90�㣬
�ߡ�BPE��90�㣬
���BPC+��EPD��90�㣬��EPD+��PED��90�㣬
���BPC����PED��
���PBC�ס�EPD��
�ߡ�PBC�ס�EPD��
�����Ʊȣ�BC��PD��
��BC��CD��PD��PC��
�����Ʊȣ�2��1��

��ϰ��ϵ�д�
�����Ŀ