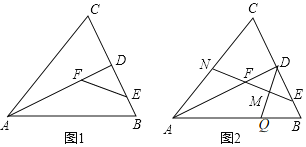
题目内容
【题目】已知函数 y1 kx ![]() ax a 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),已知函数y2 kx
ax a 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),已知函数y2 kx ![]() bx b 的图象与 x 轴交于 C、D 两点(点 C 在点 D 的左侧),其中 k 0, a b
bx b 的图象与 x 轴交于 C、D 两点(点 C 在点 D 的左侧),其中 k 0, a b
(1)求证:函数 y1 与 y2 的图象交点落在一条定直线上;
(2)若 AB=CD,求 a、b和k 满足的关系式;
(3)是否存在函数 y1 与 y2 ,使得 B,C 为线段 AD 的三等分点?若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() 且
且![]() ;(3)存在这样的函数
;(3)存在这样的函数![]() ,使得B,C为线段AD的三等分点,且
,使得B,C为线段AD的三等分点,且![]() .
.
【解析】
(1)将两函数的解析式联立求解即可得;
(2)设A、B、C、D四点的坐标,根据函数解析式分别求出四点的坐标,然后根据![]() 列出等式,进行化简即可求出a、b和k 满足的关系式;
列出等式,进行化简即可求出a、b和k 满足的关系式;
(3)由题意需分两种情况:点C在点B的左侧,此时有![]() ;点C在点B的右侧,此时有
;点C在点B的右侧,此时有![]() ;利用题(2)求出的四点坐标则可得这些线段的长度,建立等式化简求解即可.
;利用题(2)求出的四点坐标则可得这些线段的长度,建立等式化简求解即可.
(1)设交点坐标为![]()
由题意得: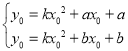
解得:![]()
![]()
![]() 即交点坐标为
即交点坐标为![]()
故函数![]() 与
与![]() 的图象交点落在定直线
的图象交点落在定直线![]() 上;
上;
(2)由题意设![]()
求解![]() 和
和![]() 两个方程可得:
两个方程可得:
![]()
则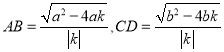
由![]() 得:
得: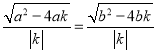
解得:![]()
即![]()
![]()
![]() 代入
代入![]() 得
得![]()
故所求的a、b和k满足的关系式为![]() 且
且![]() ;
;
(3)根据题意分以下两种情况:
①点C在点B的左侧,此时有![]() ,则
,则![]()
当![]() 时,
时,![]()
![]()
由![]() 得
得![]() ,即
,即![]()
将值代入得:![]()
解得:![]()
联立题(2)的结论得:![]()
因函数与x轴有两个交点,则![]()
两边同除以![]() 得
得![]()
此方程的根的判别式![]() ,无解
,无解
故不存在![]() ,使得B,C为线段AD的三等分点;
,使得B,C为线段AD的三等分点;
当![]() 时,
时,![]()
![]()
由![]() 得
得![]() ,即
,即![]()
将值代入得:![]()
解得:![]()
联立题(2)的结论得:![]()
因函数与x轴有两个交点,则![]()
两边同除以![]() 得
得![]()
此方程的根的判别式![]() ,无解
,无解
故不存在![]() ,使得B,C为线段AD的三等分点;
,使得B,C为线段AD的三等分点;
②点C在点B的右侧,此时有![]()
当![]() 时,
时,![]()
![]()
由![]() 得
得![]() ,即
,即![]()
将值代入得:![]()
由题(2)的结论得:![]()
联立解得:![]()
即![]()
因函数与x轴有两个交点,则![]()
两边同除以![]() 得
得![]()
解得:![]()
故存在这样的函数![]() ,使得B,C为线段AD的三等分点,且
,使得B,C为线段AD的三等分点,且![]() ;
;
当![]() 时,
时,![]()
![]()
由![]() 得
得![]() ,即
,即![]()
将值代入得:![]()
由题(2)的结论得:![]()
联立解得:![]()
即![]()
因函数与x轴有两个交点,则![]()
两边同除以![]() 得
得![]()
解得:![]()
故存在这样的函数![]() ,使得B,C为线段AD的三等分点,且
,使得B,C为线段AD的三等分点,且![]() ;
;
综上,存在这样的函数![]() ,使得B,C为线段AD的三等分点,且
,使得B,C为线段AD的三等分点,且![]() .
.

 阅读快车系列答案
阅读快车系列答案