Question

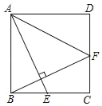
【题目】如图，在正方形ABCD中，点E是BC上一点，BF⊥AE交DC于点F，若AB＝5，BE＝2，则AF＝____．

Answer 1

【答案】.

【解析】

根据正方形的性质得到AB＝BC，∠ABE＝∠BCF＝90°，推出∠BAE＝∠EBH，根据全等三角形的性质得到CF＝BE＝2，求得DF＝5﹣2＝3，根据勾股定理即可得到结论．

∵四边形ABCD是正方形，

∴AB＝BC，∠ABE＝∠BCF＝90°，

∴∠BAE+∠AEB＝90°，

∵BH⊥AE，

∴∠BHE＝90°，

∴∠AEB+∠EBH＝90°，

∴∠BAE＝∠EBH，

在△ABE和△BCF中，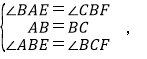

∴△ABE≌△BCF（ASA），

∴CF＝BE＝2，

∴DF＝5﹣2＝3，

∵四边形ABCD是正方形，

∴AB＝AD＝5，∠ADF＝90°，

由勾股定理得：AF＝＝＝．

故答案为：．