题目内容
 如图,AB、CD相交于点E,现给出如下三个论断:①∠A=∠C;②AD=CB;③AE=CE.请你选择其中两个论断为条件,另外一个论断为结论,构造一个真命题,并加以证明.你的选择是:
如图,AB、CD相交于点E,现给出如下三个论断:①∠A=∠C;②AD=CB;③AE=CE.请你选择其中两个论断为条件,另外一个论断为结论,构造一个真命题,并加以证明.你的选择是:
条件:________.
结论:________.
∠A=∠C,AE=CE AD=CB
分析:关键是证明△ADE≌△CBE,图形条件有对顶角相等,即∠AED=∠CEB,可利用“ASA”,“AAS”作为证明三角形全等的条件.
解答:条件:∠A=∠C,AE=CE.
结论:AD=CB.
证明:∵∠A=∠C,AE=CE,
又∵∠AED=∠CEB,
∴△ADE≌△CBE,
∴AD=CB.
故答案为:∠A=∠C,AE=CE;AD=CB.
点评:本题考查了全等三角形的判定与性质.关键是由已知条件,图形条件寻找证明三角形全等的条件.
分析:关键是证明△ADE≌△CBE,图形条件有对顶角相等,即∠AED=∠CEB,可利用“ASA”,“AAS”作为证明三角形全等的条件.
解答:条件:∠A=∠C,AE=CE.
结论:AD=CB.
证明:∵∠A=∠C,AE=CE,
又∵∠AED=∠CEB,
∴△ADE≌△CBE,
∴AD=CB.
故答案为:∠A=∠C,AE=CE;AD=CB.
点评:本题考查了全等三角形的判定与性质.关键是由已知条件,图形条件寻找证明三角形全等的条件.

练习册系列答案
相关题目
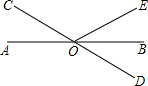 如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是
如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是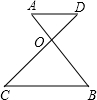 如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是
如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是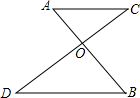 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=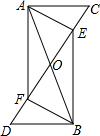 (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.
已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.