题目内容
(2012•包头)如图,拦水坝的横断面为梯形ABCD,坝顶宽AD=5米,斜 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.
(注意:本题中的计算过程和结果均保留根号)
 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.(1)求斜坡AB的长;
(2)求拦水坝的横断面梯形ABCD的周长.
(注意:本题中的计算过程和结果均保留根号)
分析:(1)根据坡度的定义得出BE的长,进而利用勾股定理得出AB的长;
(2)利用矩形性质以及坡度定义分别求出CD,CF,EF的长,进而求出梯形ABCD的周长即可.
(2)利用矩形性质以及坡度定义分别求出CD,CF,EF的长,进而求出梯形ABCD的周长即可.
解答: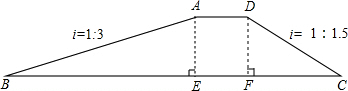 解:(1)∵
解:(1)∵
=i=
,AE=6,
∴BE=3AE=18,
在Rt△ABE中,根据勾股定理得:
AB=
=6
,
答:斜坡AB的长为6
m;
(2)过点D作DF⊥BC于F,
可得四边形AEFD是矩形,
故EF=AD,∵AD=5,∴EF=5,
∵
=i=
,
DF=AE=6,
∴CF=
DF=9,
∴BC=BE+EF+CF=18+5+9=32,
在Rt△DCF中,根据勾股定理得:
DC=
=3
,
∴梯形ABCD的周长为:AB+BC+CD+DA=6
+32+3
+5=37+6
+3
,
答:拦水坝的横断面梯形ABCD的周长为(37+6
+3
)m.
 解:(1)∵
解:(1)∵| AE |
| BE |
| 1 |
| 3 |
∴BE=3AE=18,
在Rt△ABE中,根据勾股定理得:
AB=
| AE2+BE2 |
| 10 |
答:斜坡AB的长为6
| 10 |
(2)过点D作DF⊥BC于F,
可得四边形AEFD是矩形,
故EF=AD,∵AD=5,∴EF=5,
∵
| DF |
| CF |
| 2 |
| 3 |
DF=AE=6,
∴CF=
| 3 |
| 2 |
∴BC=BE+EF+CF=18+5+9=32,
在Rt△DCF中,根据勾股定理得:
DC=
| DF2+CF2 |
| 13 |
∴梯形ABCD的周长为:AB+BC+CD+DA=6
| 10 |
| 13 |
| 10 |
| 13 |
答:拦水坝的横断面梯形ABCD的周长为(37+6
| 10 |
| 13 |
点评:此题主要考查了坡度的定义以及勾股定理的应用,根据已知坡度定义得出BE,FC的长是解题关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
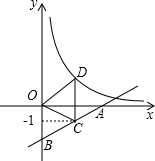 (2012•包头)如图,直线y=
(2012•包头)如图,直线y=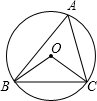 (2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为
(2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为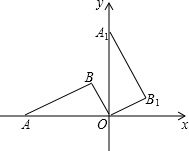 (2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为
(2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为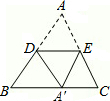 (2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论:
(2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论: