题目内容
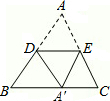（2012•包头）如图，将△ABC纸片的一角沿DE向下翻折，使点A落在BC边上的A′点处，且DE∥BC，下列结论：①∠AED=∠C；②
| A′D |
| DB |
| A′E |
| EC |
其中正确结论的个数是
4
4
个．分析：由折叠的性质可得：AD=A′D，AE=A′E，DE∥BC，易得DE是△ABC的中位线，由平行线的性质可得①∠AED=∠C与；②
=
；由三角形中位线的性质，可得③BC=2DE；由相似三角形的性质，易证得S四边形ADA′E=S△DBA′+S△EA′C．
| A′D |
| DB |
| A′E |
| EC |
解答：解：由折叠的性质可得：AD=A′D，AE=A′E，
∵DE∥BC，
∴∠AED=∠C，
故①正确；
∵DE∥BC，
∴
=
，
∴
=
，
故②正确；
∵AD=A′D，AE=A′E，DE∥BC，
∴DE是△ABC的中位线，
∴BC=2DE，
故③正确；
∵DE∥BC，
∴△ADE∽△ABC，
∴
=(
)2=
，
∴S△ADE=S△A′DE=
S△ABC，
∴S四边形ADA′E=S△DBA′+S△EA′C=
S△ABC．
故④正确．
故答案为：4．
∵DE∥BC，
∴∠AED=∠C，
故①正确；
∵DE∥BC，
∴
| AD |
| DB |
| AE |
| EC |
∴
| A′D |
| DB |
| A′E |
| EC |
故②正确；
∵AD=A′D，AE=A′E，DE∥BC，
∴DE是△ABC的中位线，
∴BC=2DE，
故③正确；
∵DE∥BC，
∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| DE |
| BC |
| 1 |
| 4 |
∴S△ADE=S△A′DE=
| 1 |
| 4 |
∴S四边形ADA′E=S△DBA′+S△EA′C=
| 1 |
| 2 |
故④正确．
故答案为：4．
点评：此题考查了折叠的性质、相似三角形的判定与性质、三角形中位线的性质以及平行线的性质．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
坡AB的坡度i=1：3（指坡面的铅直高度AE与水平宽度BE的比），斜坡DC的坡度i=1：1.5，已知该拦水坝的高为6米．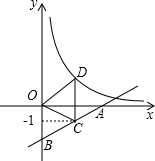
（2012•包头）如图，直线y=
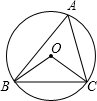（2012•包头）如图，△ABC内接于⊙O，∠BAC=60°，⊙O的半径为2，则BC的长为
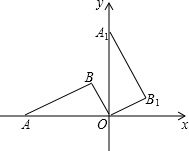（2012•包头）如图，在平面直角坐标系中，点A在x轴上，△ABO是直角三角形，∠ABO=90°，点B的坐标为（-1，2），将△ABO绕原点O顺时针旋转90°得到△A1B1O，则过A1，B两点的直线解析式为