题目内容
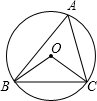 (2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为
(2012•包头)如图,△ABC内接于⊙O,∠BAC=60°,⊙O的半径为2,则BC的长为2
| 3 |
2
(保留根号).| 3 |
分析:首先过点O作OD⊥BC于D,由垂径定理可得BC=2BD,又由圆周角定理,可求得∠BOC的度数,然后根据等腰三角形的性质,求得∠OBC的度数,利用余弦函数,即可求得答案.
解答: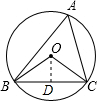 解:过点O作OD⊥BC于D,
解:过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC=60°,
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB=
=30°,
∵⊙O的半径为2,
∴BD=OB•cos∠OBC=2×
=
,
∴BC=2
.
故答案为:2
.
 解:过点O作OD⊥BC于D,
解:过点O作OD⊥BC于D,则BC=2BD,
∵△ABC内接于⊙O,∠BAC=60°,
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB=
| 180°-∠BOC |
| 2 |
∵⊙O的半径为2,
∴BD=OB•cos∠OBC=2×
| ||
| 2 |
| 3 |
∴BC=2
| 3 |
故答案为:2
| 3 |
点评:此题考查了圆周角定理、垂径定理、等腰三角形的性质以及三角函数等知识.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.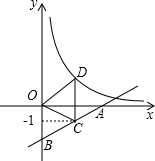 (2012•包头)如图,直线y=
(2012•包头)如图,直线y=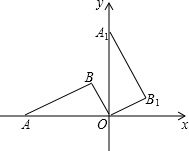 (2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为
(2012•包头)如图,在平面直角坐标系中,点A在x轴上,△ABO是直角三角形,∠ABO=90°,点B的坐标为(-1,2),将△ABO绕原点O顺时针旋转90°得到△A1B1O,则过A1,B两点的直线解析式为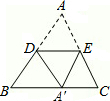 (2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论:
(2012•包头)如图,将△ABC纸片的一角沿DE向下翻折,使点A落在BC边上的A′点处,且DE∥BC,下列结论: