题目内容
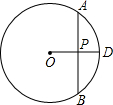如图所示，在⊙O中，OD⊥AB于P，AP=4cm，PD=2cm，则OP的长等于
- A.9cm
- B.6cm
- C.3cm
- D.1cm
C
分析：根据垂径定理、勾股定理求解．
解答：
解：连接OA，则OA2+（OD-PD）2=AP2，即OA2+（OA-2）2=42，
∴OA=5，OP=OD-PD=OA-PD=3cm．
故选C．
点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解．
分析：根据垂径定理、勾股定理求解．
解答：
解：连接OA，则OA2+（OD-PD）2=AP2，即OA2+（OA-2）2=42，∴OA=5，OP=OD-PD=OA-PD=3cm．
故选C．
点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
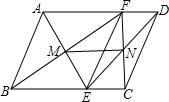如图所示，在?ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF交于点M，连接CF，DE交于点N，求证：MN∥AD且MN=
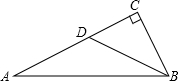如图所示，在△ABC中，∠C=90°，D是AC边上一点，且AD=DB=5，CD=3，求tan∠CBD和sinA．
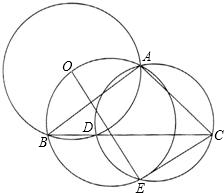如图所示，在△ABC中，已知D是BC边上的点，O为△ABD的外接圆圆心，△ACD的外接圆与△AOB的外接圆相交于A，E两点．求证：OE⊥EC．