题目内容
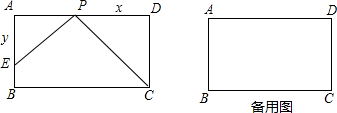
 已知矩形ABCD中,AB=1,在BC上取一点E,AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=________.
已知矩形ABCD中,AB=1,在BC上取一点E,AE将△ABE向上折叠,使B点落在AD上的F点.若四边形EFDC与矩形ABCD相似,则AD=________.

分析:可设AD=x,由四边形EFDC与矩形ABCD相似,根据相似多边形对应边的比相等列出比例式,求解即可.
解答:∵AB=1,
设AD=x,则FD=x-1,FE=1,
∵四边形EFDC与矩形ABCD相似,
∴
 =
= ,
, =
= ,
,解得x1=
 ,x2=
,x2= (不合题意舍去),
(不合题意舍去),经检验x1=
 是原方程的解.
是原方程的解.故答案为
 .
.点评:本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据四边形EFDC与矩形ABCD相似得到比例式.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
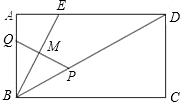
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.