题目内容
如图所示,已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点(与A、D不重合),过点P作PE⊥CP交直线AB于点E,设PD=x,AE=y,(1)写出y与x的函数解析式,并指出自变量的取值范围;
(2)如果△PCD的面积是△AEP面积的4倍,求CE的长;
(3)是否存在点P,使△APE沿PE翻折后,点A落在BC上?证明你的结论.
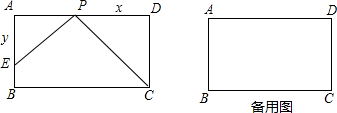
分析:(1)运用三角形相似,对应边比值相等即可解决,
(2)运用三角形面积的关系得出,对应边的关系,即可解决,
(3)根据相似三角形的判定得出
=
,进而求出关于x的方程,利用根的判别式求出即可.
(2)运用三角形面积的关系得出,对应边的关系,即可解决,
(3)根据相似三角形的判定得出
| OA |
| PA |
| PD |
| PC |
解答: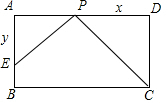 (1)解:∵PE⊥CP,
(1)解:∵PE⊥CP,
∴可得:△EAP∽△PDC,
∴
=
,
又∵CD=2,AD=3,设PD=x,
AE=y,
∴
=
,
∴y=-
x2+
x,
0<x<3;
(2)解:当△PCD的面积是△AEP面积的4倍,
则:相似比为2:1,
∴
=
=
,
∵CD=2,
∴AP=1,PD=2,
∴PE=
,PC=2
,
∴EC=
.
(3)不存在.
作AF⊥PE,交PE于O,BC于F,连接EF
∵AF⊥PE,CP⊥PE
∴AF=CP=
,
PE=
,
∵△CDP∽△POA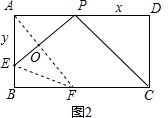
∴
=
,
OA=
,
若OA=
AF
=
,
3x2-6x+4=0
△=62-4×4×3=-12
x无解
因此,不存在.
 (1)解:∵PE⊥CP,
(1)解:∵PE⊥CP,∴可得:△EAP∽△PDC,
∴
| AE |
| PD |
| PA |
| CD |
又∵CD=2,AD=3,设PD=x,
AE=y,
∴
| y |
| x |
| 3-x |
| 2 |
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
0<x<3;
(2)解:当△PCD的面积是△AEP面积的4倍,
则:相似比为2:1,
∴
| AE |
| PD |
| AP |
| CD |
| 1 |
| 2 |
∵CD=2,
∴AP=1,PD=2,
∴PE=
| 2 |
| 2 |
∴EC=
| 10 |
(3)不存在.
作AF⊥PE,交PE于O,BC于F,连接EF
∵AF⊥PE,CP⊥PE
∴AF=CP=
| x2+22 |
PE=
| (3-x)2+y2 |
∵△CDP∽△POA

∴
| OA |
| PA |
| PD |
| PC |
OA=
| (3-x)x | ||
|
若OA=
| 1 |
| 2 |
| (3-x)x | ||
|
| 1 |
| 2 |
| x2+22 |
3x2-6x+4=0
△=62-4×4×3=-12
x无解
因此,不存在.
点评:此题主要考查了相似三角形的判定,以及相似三角形面积比是相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
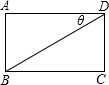 如图所示,已知矩形ABCD(AD>AB)中,AB=a,∠BDA=θ,试用a与θ表示:AD=
如图所示,已知矩形ABCD(AD>AB)中,AB=a,∠BDA=θ,试用a与θ表示:AD=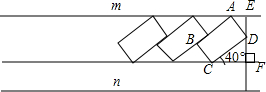
 如图所示,已知矩形ABCD的边AB=3cm,AD=4cm.
如图所示,已知矩形ABCD的边AB=3cm,AD=4cm. 如图所示,已知矩形ABCD中两条对角线AC、BD相交于点O,∠ADB=30°,DF∥AC交BC的延长线于F点,
如图所示,已知矩形ABCD中两条对角线AC、BD相交于点O,∠ADB=30°,DF∥AC交BC的延长线于F点,