题目内容
【题目】已知:如图,AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°. 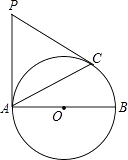
(1)求∠P的大小;
(2)若AB=6,求PA的长.
【答案】
(1)解:∵PA是⊙O的切线,AB为⊙O的直径,
∴PA⊥AB,即∠PAB=90°.
∵∠BAC=30°,
∴∠PAC=90°﹣30°=60°.
又∵PA、PC切⊙O于点A、C,
∴PA=PC,
∴△PAC是等边三角形,
∴∠P=60°
(2)解:如图,连接BC.
∵AB是直径,∠ACB=90°,
∴在Rt△ACB中,AB=6,∠BAC=30°,
可得AC=ABcos∠BAC=6×cos30°=3 ![]() .
.
又∵△PAC是等边三角形,
∴PA=AC=3 ![]() .
.
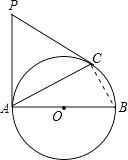
【解析】(1)由圆的切线的性质,得∠PAB=90°,结合∠BAC=30°得∠PAC=90°﹣30°=60°.由切线长定理得到PA=PC,得△PAC是等边三角形,从而可得∠P=60°.(2)连接BC,根据直径所对的圆周角为直角,得到∠ACB=90°,结合Rt△ACB中AB=6且∠BAC=30°,得到AC=ABcos∠BAC=3 ![]() .最后在等边△PAC中,可得PA=AC=3
.最后在等边△PAC中,可得PA=AC=3 ![]() .
.
【考点精析】根据题目的已知条件,利用切线的性质定理的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目