题目内容
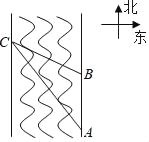
【题目】在一次数学活动课上,老师带领学生测量一条南北流向的河的宽度,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行10米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到1米,参考数值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)
【答案】15米
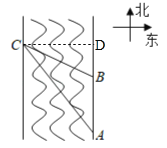
【解析】分析:过点C作CD⊥AB于D,由题意知道∠DAC=31°,∠DBC=45°,设CD=BD=x米,则AD=AB+BD=(10+x)米.在Rt△ACD中,tan∠DAC=![]() ,由此可以列出关于x的方程,解方程即可求解.
,由此可以列出关于x的方程,解方程即可求解.
详解:过点C作CD⊥AB,垂足为D.
设CD=x米.在Rt△BCD中,∠CBD=45°,∴BD=CD=x米.
在Rt△ACD中,∠DAC=31°,AD=AB+BD=(10+x)米,CD=x米.
∵tan∠DAC=![]() =
=![]() ,解得:x=15.
,解得:x=15.
经检验x=15是原方程的解,且符合题意.
答:这条河的宽度为15米.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目