题目内容
如图,点P是⊙O上任意一点,⊙O的弦AB所在的直线与⊙P相切于点C,PF为⊙O的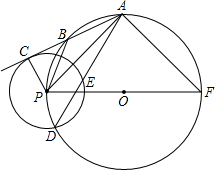 直径,设⊙O与⊙P的半径分别为R和r.
直径,设⊙O与⊙P的半径分别为R和r.(1)求证:△PCB∽△PAF;
(2)求证:PA•PB=2Rr;
(3)若点D是两圆的一个交点,连接AD交⊙P于点E,当R=3r,PA=6,PB=3时,求⊙P的弦DE的长.
分析:(1)根据切线的性质知∠PCB=90°、直径所对的圆周角∠PAF=90°,∠PBC=∠F,易得△PCB∽△PAF;
(2)由(1)所得结论PA•PB=PC•PF即PA•PB=2Rr;
(3)求⊙P的弦DE的长是一个较复杂的问题,可先作出弦DE的弦心距PH.通过解直角三角形来求.
(2)由(1)所得结论PA•PB=PC•PF即PA•PB=2Rr;
(3)求⊙P的弦DE的长是一个较复杂的问题,可先作出弦DE的弦心距PH.通过解直角三角形来求.
解答:(1)证明:∵AC切⊙P于C,PF为⊙O的直径,
∴∠PCB=∠PAF=90°,
又∵∠CBP=∠F,
∴△PCB∽△PAF.
(2)证明:∵△PCB∽△PAF,
∴
=
,
∴PA•PB=PC•PF=2Rr;
(3)解:连接PD,过点P作PH⊥DE于H.
∵∠PCB=∠PHD=90°,∠CBP=∠F=∠HDP,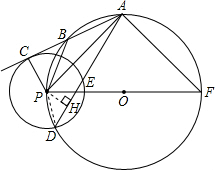
∴△CBP∽△HDP,
∴
=
.
∴PH•PB=PC•PD.
又∵PC=PD=r,
∴PH•PB=r2,
∴PH=
.
∵PA=6,PB=3,
由(2)知PA•PB=2Rr,
∴r=
,R=3
.
∴PH=
=
=1.
∴DH=
=
-1=
,
∴DE=2
.
∴∠PCB=∠PAF=90°,
又∵∠CBP=∠F,
∴△PCB∽△PAF.
(2)证明:∵△PCB∽△PAF,
∴
| PC |
| PB |
| PA |
| PF |
∴PA•PB=PC•PF=2Rr;
(3)解:连接PD,过点P作PH⊥DE于H.
∵∠PCB=∠PHD=90°,∠CBP=∠F=∠HDP,

∴△CBP∽△HDP,
∴
| PC |
| PH |
| PB |
| PD |
∴PH•PB=PC•PD.
又∵PC=PD=r,
∴PH•PB=r2,
∴PH=
| r2 |
| PB |
∵PA=6,PB=3,
由(2)知PA•PB=2Rr,
∴r=
| 3 |
| 3 |
∴PH=
| r2 |
| PB |
(
| ||
| 3 |
∴DH=
| PD2-PH2 |
| 3 |
| 2 |
∴DE=2
| 2 |
点评:本题综合考查了相似三角形是判定与性质、圆内接四边形的性质及切线的性质.解第(1)、(2)问的解决运用了以下知识:切线的性质,圆周角定理的推论,圆的内接四边形的性质.由此可以看出在两圆的位置关系问题中,综合知识的运用是至关重要的;第(3)问求弦DE的长是一个较复杂的问题,但还是离不开前面的基本知识“弦和弦心距亲密紧相连”,由此可以看出解决问题的基本模式是相当重要的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点P是反比例函数y=
如图,点P是反比例函数y=| 1 |
| x |
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、
|
 9、按题目要求画图,并回答相关问题.
9、按题目要求画图,并回答相关问题. 已知如图,点A是反比例函数y=
已知如图,点A是反比例函数y= (2013•燕山区一模)如图,点P是⊙O的弦AB上任一点(与A,B均不重合),点C在⊙O上,PC⊥OP,已知AB=8,设BP=x,PC2=y,y与x之间的函数图象大致是( )
(2013•燕山区一模)如图,点P是⊙O的弦AB上任一点(与A,B均不重合),点C在⊙O上,PC⊥OP,已知AB=8,设BP=x,PC2=y,y与x之间的函数图象大致是( )