ΧβΡΩΡΎ»ί
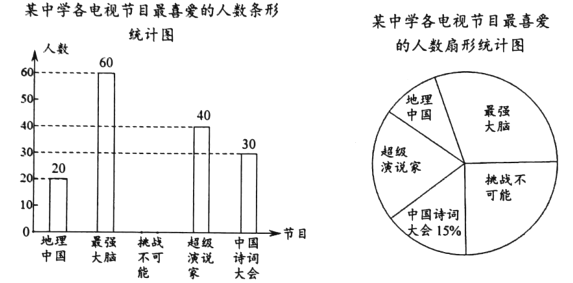
ΓΨΧβΡΩΓΩΘ®2017ΦΟΡΰΘ§ΒΎ21ΧβΘ§9Ζ÷Θ©“―÷ΣΚ· ΐ![]() ΒΡΆΦœσ”κx÷α”–ΝΫΗωΙΪΙ≤ΒψΘ°
ΒΡΆΦœσ”κx÷α”–ΝΫΗωΙΪΙ≤ΒψΘ°
Θ®1Θ©«σmΒΡ»Γ÷ΒΖΕΈßΘ§≤Δ–¥≥ωΒ±m»ΓΖΕΈßΡΎΉν¥σ’ϊ ΐ ±Κ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΧβΘ®1Θ©÷–«σΒΟΒΡΚ· ΐΦ«ΈΣC1Θ°
ΔΌΒ±nΓήxΓή©¹1 ±Θ§yΒΡ»Γ÷ΒΖΕΈß «1ΓήyΓή©¹3nΘ§«σnΒΡ÷ΒΘΜ
ΔΎΚ· ΐ![]() ΒΡΆΦœσ”…Κ· ΐC1ΒΡΆΦœσΤΫ“ΤΒΟΒΫΘ§ΤδΕΞΒψP¬δ‘Ύ“‘‘≠ΒψΈΣ‘≤–ΡΘ§ΑκΨΕΈΣ
ΒΡΆΦœσ”…Κ· ΐC1ΒΡΆΦœσΤΫ“ΤΒΟΒΫΘ§ΤδΕΞΒψP¬δ‘Ύ“‘‘≠ΒψΈΣ‘≤–ΡΘ§ΑκΨΕΈΣ![]() ΒΡ‘≤ΡΎΜρ‘≤…œΘ§…ηΚ· ΐC1ΒΡΆΦœσΕΞΒψΈΣMΘ§«σΒψP”κΒψMΨύάκΉν¥σ ±Κ· ΐC2ΒΡΫβΈω ΫΘ°
ΒΡ‘≤ΡΎΜρ‘≤…œΘ§…ηΚ· ΐC1ΒΡΆΦœσΕΞΒψΈΣMΘ§«σΒψP”κΒψMΨύάκΉν¥σ ±Κ· ΐC2ΒΡΫβΈω ΫΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©mΘΦ![]() «“mΓΌ0Θ§
«“mΓΌ0Θ§![]() ΘΜΘ®2Θ©ΔΌ©¹2ΘΜΔΎ
ΘΜΘ®2Θ©ΔΌ©¹2ΘΜΔΎ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©Κ· ΐΆΦ–Έ”κx÷α”–ΝΫΗωΙΪΙ≤ΒψΘ§‘ρΗΟΚ· ΐΈΣΕΰ¥ΈΚ· ΐ«“ΓςΘΨ0Θ§Ι ¥ΥΩ…ΒΟΒΫΙΊ”ΎmΒΡ≤ΜΒ» ΫΉιΘ§¥”ΕχΩ…«σΒΟmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©œ»«σΒΟ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΘ§Β±nΓήxΓή©¹1 ±Θ§Κ· ΐΆΦœσΈΜ”ΎΕ‘≥Τ÷αΒΡΉσ≤ύΘ§yΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§Β±Β±x=n ±Θ§y”–Ήν¥σ÷Β©¹3nΘ§»ΜΚσΫΪx=nΘ§y=©¹3n¥ζ»κ«σΫβΦ¥Ω…ΘΜ
Θ®3Θ©œ»«σΒΟΒψMΒΡΉχ±ξΘ§»ΜΚσ‘Ό«σΒΟΒ±MPΨ≠Ιΐ‘≤–Ρ ±Θ§PM”–Ήν¥σ÷ΒΘ§Ι ¥ΥΩ…«σΒΟΒψPΒΡΉχ±ξΘ§¥”ΕχΩ…ΒΟΒΫΚ· ΐC2ΒΡΫβΈω ΫΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏΚ· ΐΆΦœσ”κx÷α”–ΝΫΗωΫΜΒψΘ§ΓύmΓΌ0«“[©¹Θ®2m©¹5Θ©]2©¹4mΘ®m©¹2Θ©ΘΨ0Θ§ΫβΒΟΘΚmΘΦ![]() «“mΓΌ0Θ°
«“mΓΌ0Θ°
ΓΏmΈΣΖϊΚœΧθΦΰΒΡΉν¥σ’ϊ ΐΘ§Γύm=2Θ§ΓύΚ· ΐΒΡΫβΈω ΫΈΣ![]() Θ°
Θ°
Θ®2Θ©≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣx=![]() =
=![]() Θ°
Θ°
ΓΏnΓήxΓή©¹1ΘΦ![]() Θ§a=2ΘΨ0Θ§ΓύΒ±nΓήxΓή©¹1 ±Θ§yΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§ΓύΒ±x=n ±Θ§y=©¹3nΘ§Γύ2n2+n=©¹3nΘ§ΫβΒΟn=©¹2Μρn=0Θ®…α»ΞΘ©Θ§ΓύnΒΡ÷ΒΈΣ©¹2Θ°
Θ§a=2ΘΨ0Θ§ΓύΒ±nΓήxΓή©¹1 ±Θ§yΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§ΓύΒ±x=n ±Θ§y=©¹3nΘ§Γύ2n2+n=©¹3nΘ§ΫβΒΟn=©¹2Μρn=0Θ®…α»ΞΘ©Θ§ΓύnΒΡ÷ΒΈΣ©¹2Θ°
Θ®3Θ©ΓΏ![]() =
=![]() Θ§ΓύMΘ®
Θ§ΓύMΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
»γΆΦΥυ ΨΘΚ
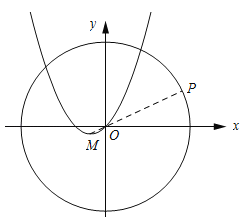
Β±ΒψP‘ΎOM”κΓ―OΒΡΫΜΒψ¥Π ±Θ§PM”–Ήν¥σ÷ΒΘ°
…η÷±œΏOMΒΡΫβΈω ΫΈΣy=kxΘ§ΫΪΒψMΒΡΉχ±ξ¥ζ»κΒΟΘΚ![]() Θ§ΫβΒΟΘΚk=
Θ§ΫβΒΟΘΚk=![]() Θ§ΓύOMΒΡΫβΈω ΫΈΣy=
Θ§ΓύOMΒΡΫβΈω ΫΈΣy=![]() xΘ°
xΘ°
…ηΒψPΒΡΉχ±ξΈΣΘ®xΘ§![]() xΘ©Θ°
xΘ©Θ°
”…ΝΫΒψΦδΒΡΨύάκΙΪ ΫΩ…÷ΣΘΚOP=![]() =5Θ§ΫβΒΟΘΚx=2Μρx=©¹2Θ®…α»ΞΘ©Θ§ΓύΒψPΒΡΉχ±ξΈΣΘ®2Θ§1Θ©Θ§ΓύΒ±ΒψP”κΒψMΨύάκΉν¥σ ±Κ· ΐC2ΒΡΫβΈω ΫΈΣ
=5Θ§ΫβΒΟΘΚx=2Μρx=©¹2Θ®…α»ΞΘ©Θ§ΓύΒψPΒΡΉχ±ξΈΣΘ®2Θ§1Θ©Θ§ΓύΒ±ΒψP”κΒψMΨύάκΉν¥σ ±Κ· ΐC2ΒΡΫβΈω ΫΈΣ![]() Θ°
Θ°

ΓΨΧβΡΩΓΩΡ≥ΒγΤς≥§ –œζ έΟΩΧ®ΫχΦέΖ÷±πΈΣ160‘ΣΓΔ120‘ΣΒΡAΓΔBΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»Θ§»γ±μ «ΫϋΝΫ÷ήΒΡœζ έ«ιΩωΘΚΘ®ΫχΦέΓΔ έΦέΨυ±Θ≥÷≤Μ±δΘ§άϊ»σ=œζ έ ’»κ©¹ΫχΜθ≥…±ΨΘ©
œζ έ ±ΕΈ | œζ έ ΐΝΩ | œζ έ ’»κ | |
A÷÷–ΆΚ≈ | B÷÷–ΆΚ≈ | ||
ΒΎ“Μ÷ή | 3Χ® | 4Χ® | 1200‘Σ |
ΒΎΕΰ÷ή | 5Χ® | 6Χ® | 1900‘Σ |
Θ®1Θ©«σAΓΔBΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»ΒΡœζ έΒΞΦέΘΜ
Θ®2Θ©»τ≥§ –ΉΦ±Η”Ο≤ΜΕύ”Ύ7500‘ΣΒΡΫπΕν‘Ό≤…ΙΚ’βΝΫ÷÷–ΆΚ≈ΒΡΒγΖγ…»Ι≤50Χ®Θ§«σA÷÷–ΆΚ≈ΒΡΒγΖγ…»ΉνΕύΡή≤…ΙΚΕύ…ΌΧ®ΘΩ