Question

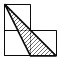
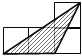
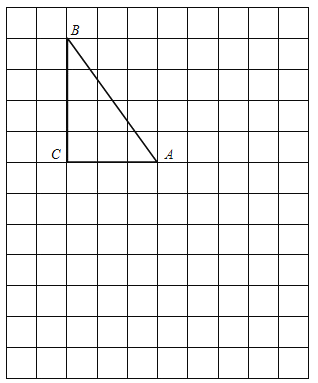
【题目】在如图网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4．

（1）试在图中作出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；

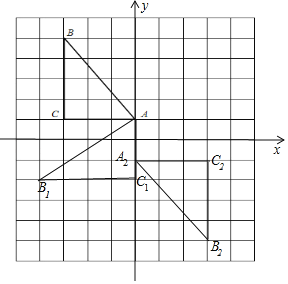
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并直接写出A、C两点的坐标；

（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并直接写出点A2、B2、C2的坐标．

Answer 1

【答案】（1）见解析；

（2）（0，1），（﹣3，1）；

（3）（0，﹣1），（3，﹣5），（3，﹣1）．

【解析】

（1）利用网格特点和旋转的性质画出B、C的对应点B1、C1即可；

（2）利用B点坐标画出直角坐标系，然后写出A、C的坐标；

（3）利用关于原点对称的点的坐标特征写出点A2、B2、C2的坐标，然后描点即可．

解：（1）如图，△AB1C1为所作；

（2）如图，A点坐标为（0，1），C点的坐标为（﹣3，1）；

（3）如图，△A2B2C2为所作，点A2、B2、C2的坐标烦恼为（0，﹣1），（3，﹣5），（3，﹣1）．