题目内容
【题目】已知关于x的一元二次方程x2+mx﹣6＝0．
（1）求证：不论m为何实数，方程总有两个不相等的实数根；
（2）若m＝1，用配方法解这个一元二次方程．
【答案】（1）见解析，（2）x1＝2，x2＝﹣3．
【解析】
（1）根据方程的系数结合根的判别式，可得出△=m2+24＞0，进而即可证出：不论m为何实数，方程总有两个不相等的实数根；
（2）代入m=1，根据配方法解一元二次方程的步骤求解，即可得出结论．
解：（1）证明：△＝m2﹣4×1×（﹣6）＝m2+24．
∵m2≥0，
∴m2+24＞0，即△＞0，
∴不论m为何实数，方程总有两个不相等的实数根；
（2）解：当m＝1时，原方程为x2+x﹣6＝0，
移项，得：x2+x＝6，
配方，得：x2+2×
x+（）2＝6+（）2，即（x+）2＝（
）2，
开方，得：x+＝±，
∴x1＝2，x2＝﹣3．
学习实践园地系列答案
【题目】某校初三体育考试选择项目中，选择篮球项目和排球项目的学生比较多
为了解学生掌握篮球技巧和排球技巧的水平情况，进行了抽样调查，过程如下，请补充完整．
收集数据从选择篮球和排球的学生中各随机抽取16人，进行了体育测试，测试成绩
十分制
如下：
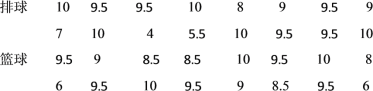
整理、描述数据按如下分数段整理、描述这两组样本数据：
|
|
|
| 10 | |
排球 | 1 | 1 | 2 | 7 | 5 |
篮球 |
说明：成绩
分及以上为优秀，6分及以上为合格，6分以下为不合格
分析数据两组样本数据的平均数、中位数、众数如下表所示：
项目 | 平均数 | 中位数 | 众数 |
排球 |
|
| 10 |
篮球 |
|
|
|
得出结论
如果全校有160人选择篮球项目，达到优秀的人数约为______人；
初二年级的小明和小军看到上面数据后，小明说：排球项目整体水平较高小军说：篮球项目整体水平较高．
你同意______的看法，理由为______
至少从两个不同的角度说明推断的合理性
【题目】已知y是x的函数，自变量x的取值范围是x≠0的全体实数，如表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
（1）从表格中读出，当自变量是﹣2时，函数值是 ；
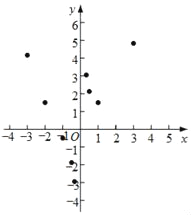
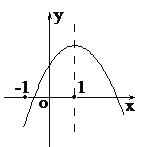
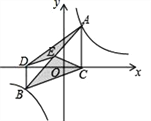
（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（3）在画出的函数图象上标出x＝2时所对应的点，并写出m＝ ．
（4）结合函数的图象，写出该函数的一条性质： ．
