Question

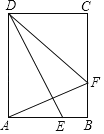
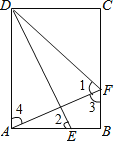
【题目】在矩形ABCD中，BC＝10cm、DC＝6cm，点E、F分别为边AB、BC上的两个动点，E从点A出发以每秒5cm的速度向B运动，F从点B出发以每秒3cm的速度向C运动，设运动时间为t秒．若∠AFD＝∠AED，则t的值_____．

Answer 1

【答案】

【解析】

根据题意知AE＝5t、BF＝3t，证出＝，且∠DAE＝∠ABF＝90°，证△ADE∽△BAF得∠2＝∠3，结合∠3＝∠4、∠1＝∠2得∠1＝∠4，即可知DF＝DA，从而得62+（10﹣3t）2＝102，解之可得t的值，继而根据0≤5t≤6且0≤3t≤10取舍可得答案．

解：如图，

∵四边形ABCD是矩形，

∴AB＝DC＝6cm，AD＝BC＝10cm，

根据题意知，AE＝5t，BF＝3t，

∵BC＝10cm，DC＝6cm，

∴＝＝，＝＝，

∴＝，

又∵∠DAE＝∠ABF＝90°，

∴△ADE∽△BAF，

∴∠2＝∠3，

∵AD∥BC，

∴∠3＝∠4，

∴∠2＝∠4，

∵∠1＝∠2，

∴∠1＝∠4，

∴DF＝DA，即DF2＝AD2，

∵BF＝3t，BC＝10，

∴CF＝10﹣3t，∴DF2＝DC2+CF2，即DF2＝62+（10﹣3t）2，

∴62+（10﹣3t）2＝102，

解得：t＝或t＝6，

∵0≤5t≤6且0≤3t≤10，

∴0≤t≤，

∴t＝，

故答案为：.