题目内容
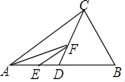
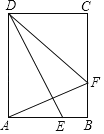
【题目】如图,已知BD:OD=2:1,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
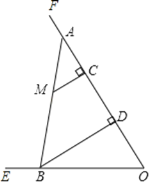
(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
【答案】(1)2或8;(2)△ABO为直角三角形,理由见解析;(3)18
【解析】
(1)由于∠MCA=∠BDO=90°,所以△AMC和△BOD相似时分两种情况:①△AMC∽△BOD;②△AMC∽△OBD.则两种情况都可以根据相似三角形对应边的比相等列出关于AC的方程,解方程即可求出AC的长度;
(2)先由MC∥BD,得出△AMC∽△ABD,根据相似三角形对应边的比相等及三角形中位线的性质求出BD=2MC=8,OD=4,CD=8,AC=CD=8,再利用SAS证明△AMC≌△BOD,得到∠CAM=∠DBO,根据平行线的性质及三角形内角和定理求出∠ABO=90°,进而得出△ABO为直角三角形;
(3)设OD=a,根据tan∠EOF=2得出BD=2a,由三角形的面积公式求出S△AMC=2AC,S△BOC=12a,根据S△AMC=S△BOC,得到AC=6a.由△AMC∽△ABD,根据相似三角形对应边的比相等列出关于a的方程,解方程求出a的值,进而得出AC的长.
解:(1)∵∠MCA=∠BDO=90°,
∴△AMC和△BOD中,C与D是对应点,
∴△AMC和△BOD相似时分两种情况:
①当△AMC∽△BOD时,![]() =
=![]() =2,
=2,
∵MC=4,
∴![]() =2,
=2,
解得AC=8;
②当△AMC∽△OBD时,![]() =
=![]() =2,
=2,
∵MC=4,
∴![]() =2,
=2,
解得AC=2.
故当AC的长度为2或8时,△AMC和△BOD相似;
(2)△ABO为直角三角形.理由如下:
∵MC∥BD,
∴△AMC∽△ABD,
∴![]() =
=![]() =
=![]() ,∠AMC=∠ABD,
,∠AMC=∠ABD,
∵M为AB中点,
∴C为AD中点,BD=2MC=8.
∵BD:OD=2:1,
∴OD=4,
∴CD=OC﹣OD=8,
∴AC=CD=8.
在△AMC与△BOD中,
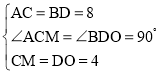 ,
,
∴△AMC≌△BOD(SAS),
∴∠CAM=∠DBO,
∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°,
∴△ABO为直角三角形;
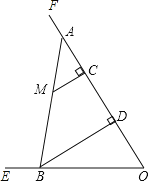
(3)连结BC,设OD=a,则BD=2a.
∵S△AMC=S△BOC,S△AMC=![]() ACMC=2AC,S△BOC=
ACMC=2AC,S△BOC=![]() OCBD=12a,
OCBD=12a,
∴2AC=12a,
∴AC=6a.
∵△AMC∽△ABD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得a1=3,a2=﹣![]() (舍去),
(舍去),
∴AC=6×3=18.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案