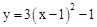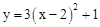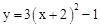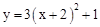题目内容
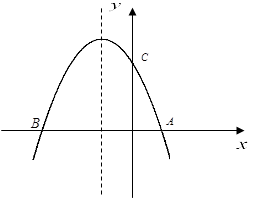
如图,抛物线 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),
(1)求该抛物线的解析式;
(2)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),
(1)求该抛物线的解析式;
(2)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
抛物线解析式为:y=-x2-2x+3;点P坐标为



试题分析:(1)根据题意可知,将点A、B代入函数解析式,列得方程组即可求得b、c的值,求得函数解析式;
(2)存在,设得点P的坐标,将△BCP的面积表示成二次函数,根据二次函数最值的方法即可求得点P的坐标.
试题解析:

解:(1)将A(1,0),C(0,3)代y=-x2+bx+c中得

∴

∴抛物线解析式为:y=-x2-2x+3;
(2)存在.
把B(m,0)代入y=-x2-2x+3;得:m=-3
∴

理由如下:设P点(x,-x2-2x+3)(-3<x<0)
∵

若S四边形BPCO有最大值,则S△BPC就最大,
∴




当
 时,
时,
∴

当

时,

∴点P坐标为
 .
.
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目

 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
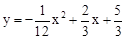 ,则铅球推出距离 米.
,则铅球推出距离 米.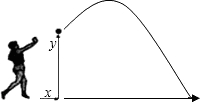
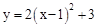 的图象的顶点坐标是( )
的图象的顶点坐标是( )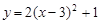 的顶点坐标是( )
的顶点坐标是( )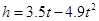 (的单位:秒,
(的单位:秒, 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )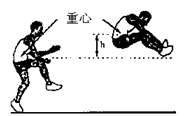
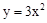 向左平移2个单位,再向下平移1个单位,所得抛物线为
向左平移2个单位,再向下平移1个单位,所得抛物线为