题目内容
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
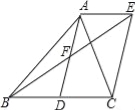
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
【答案】(1)证明见解析(2)当AB=AC时(3)当AB=AC,AB⊥AC时
【解析】
试题分析:(1)首先证明△AFE≌△DFB可得AE=BD,进而可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)当AB=AC时,根据等腰三角形三线合一可得AD⊥BC,再根据有一个角是直角的平行四边形是矩形可得结论;
(3)当AB=AC,AB⊥AC时,△ABC是等腰直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得AD=CD,根据等腰三角形的性质可得AD⊥BC,从而可得证明四边形ADCE是正方形.
试题解析: (1)∵AD是△ABC的中线,
∴BD=CD,
∵AE∥BC,
∴∠AEF=∠DBF,
在△AFE和△DFB中,
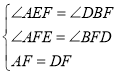 ,
,
∴△AFE≌△DFB(AAS),
∴AE=BD,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形;
(2)当AB=AC时,四边形ADCE是矩形;
∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
故答案为:AB=AC;
(3)当AB⊥AC,AB=AC时,四边形ADCE是正方形,
∵AB⊥AC,AB=AC,
∴△ABC是等腰直角三角形,
∵AD是△ABC的中线,
∴AD=CD,AD⊥BC,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是正方形,
故答案为:AB⊥AC,AB=AC.

【题目】某商场一名业务员12个月的销售额(单位:万元)如下表:
月份(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
销售额(万元) | 6.2 | 9.8 | 9.8 | 7.8 | 7.2 | 6.4 | 9.8 | 8 | 7 | 9.8 | 10 | 7.5 |
则这组数据的众数和中位数分别是( )
A. 10,8 B. 9.8,9.8 C. 9.8,7.9 D. 9.8,8.1
