题目内容
【题目】如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B的坐标分别为(-2,0),(![]() ,0),AD=2,∠DAB=60°点P从点A出发沿A→D→C运动到点C,连接PO.当PO=OB时,点P的坐标为___.
,0),AD=2,∠DAB=60°点P从点A出发沿A→D→C运动到点C,连接PO.当PO=OB时,点P的坐标为___.

【答案】(-![]() ,
,![]() )或(0,
)或(0,![]() )
)
【解析】
作OF⊥AD于F,作PE⊥OA于E,由直角三角形的性质得出![]() ,证出∠AOP=30°,得出PE=
,证出∠AOP=30°,得出PE=![]() OP=
OP=![]() ,OE=
,OE=![]() PE=
PE=![]() ,得出
,得出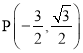 ;设CD与y轴交于Q,连接OD,由等边三角形的性质得出∠AOD=60°,由直角三角形的性质得出DQ=
;设CD与y轴交于Q,连接OD,由等边三角形的性质得出∠AOD=60°,由直角三角形的性质得出DQ=![]() OD=1,OQ=
OD=1,OQ=![]() DQ=
DQ=![]() ,得出Q(0,
,得出Q(0,![]() );即可得出结果.
);即可得出结果.
作OF⊥AD于F,作PE⊥OA于E,如图所示:
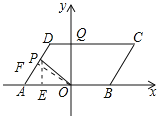
则∠AOF=30°,
∴AF=![]() OA=1,
OA=1,
∴OF=![]() AF=
AF=![]() ,
,
∴F与P重合,
∴∠OPA=90°,
∴∠AOP=30°,
∴PE=![]() OP=
OP=![]() ,OE=
,OE=![]() PE=
PE=![]() ,
,
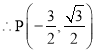 ;
;
设CD与y轴交于Q,连接OD,
∵∠BAD=60°,
∴△AOD是等边三角形,
∴∠AOD=60°,
∴∠DOQ=30°,OD=OA=2,
∴DQ=![]() OD=1,
OD=1,
∴OQ=![]() DQ=
DQ=![]() ,
,
∴OQ=OB,
∴Q(0,![]() );
);
当PO=OB时,点P的坐标为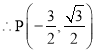 或(0,
或(0,![]() ).
).

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
【题目】某超市在“十一”长假期间对顾客实行优惠,规定如下:
一次性购物金额 | 优惠办法 |
不超过100元 | 不予优惠 |
超过100元但不超过500元 | 超过100元部分给予九折优惠 |
超过500元 | 超过500元部分给予八折优惠 |
(1)小明的爷爷一次性购200元的保健食品,他实际付款_____元;小明妈妈一次性购300元的衣服,她实际付款_____元;如果他们两人合作付款,则能少付_____元;
(2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她实际付款_____元;(用含x的式子表示,写最简结果)
(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(![]() ),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)
),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)