题目内容
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．（1）则四边形DBCE是
梯
梯
形（填写：平行四边形、矩形、菱形、正方形、梯形）（2）若AB=AC=1，BC=
| 3 |
分析：（1）由等腰三角形的性质与旋转的性质，易证得∠DEB=∠ABC=α，即可得DE∥BC，又由DE=AC≠BC，可得四边形DBCE是梯形；
（2）首先过点A作AF⊥BC于点F，过点D作DH⊥BC于点H，由等腰三角形的性质，易求得BF的长，然后由特殊角的三角函数值，可求得α的度数，∠DBH的度数，则可求得DH的长，继而求得四边形DBCE的面积．
（2）首先过点A作AF⊥BC于点F，过点D作DH⊥BC于点H，由等腰三角形的性质，易求得BF的长，然后由特殊角的三角函数值，可求得α的度数，∠DBH的度数，则可求得DH的长，继而求得四边形DBCE的面积．
解答：解：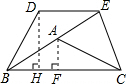
（1）∵AB=AC，∠ABC=α，
∴∠ACB=∠ABC=α，
由旋转的性质可得：∠BED=∠ACB=α，DE=AC，
∴∠BED=∠ABC，
∴BC∥DE，
∵BC≠AC，
∴BC≠DE，
∴四边形DBCE是梯形；
故答案为：梯；
（2）过点A作AF⊥BC于点F，过点D作DH⊥BC于点H，
∵AB=AC=1，
∴BF=FC=
BC=
，
∴cosα=
，
∴∠ABC=30°，
∴∠DBC=60°，
∵将△ABC以点B为旋转中心逆时针旋转α度角（0°＜α＜90°），得到△BDE，
∴△ABC≌△DBE，
∴BD=DE=1，
∴DH=BD•sin60°=
，
∴S梯形DBCE=
(1+
)
=
．
（1）∵AB=AC，∠ABC=α，∴∠ACB=∠ABC=α，
由旋转的性质可得：∠BED=∠ACB=α，DE=AC，
∴∠BED=∠ABC，
∴BC∥DE，
∵BC≠AC，
∴BC≠DE，
∴四边形DBCE是梯形；
故答案为：梯；
（2）过点A作AF⊥BC于点F，过点D作DH⊥BC于点H，
∵AB=AC=1，
∴BF=FC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴cosα=
| ||
| 2 |
∴∠ABC=30°，
∴∠DBC=60°，
∵将△ABC以点B为旋转中心逆时针旋转α度角（0°＜α＜90°），得到△BDE，
∴△ABC≌△DBE，
∴BD=DE=1，
∴DH=BD•sin60°=
| ||
| 2 |
∴S梯形DBCE=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
3+
| ||
| 4 |
点评：此题考查了梯形的判定与性质、旋转的性质、等腰三角形的性质以及特殊角的三角函数值．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
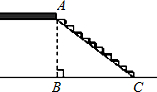（2012•通州区一模）某地区准备修建一座高AB=6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为
（2012•通州区一模）已知四边形ABCD，点E是射线BC上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交射线AC于点P，连接DP，PE．
（2012•通州区一模）如图，BD是⊙O的弦，点C在BD上，以BC为边作等边三角形△ABC，点A在圆内，且AC恰好经过点O，其中BC=12，OA=8，则BD的长为（ ）