题目内容
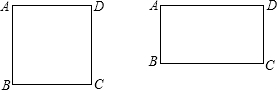 (2012•通州区一模)已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,连接DP,PE.
(2012•通州区一模)已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,连接DP,PE.(1)若四边形ABCD是正方形,猜想PD与PE的关系,并证明你的结论.
(2)若四边形ABCD是矩形,(1)中的PD与PE的关系还成立吗?
不成立
不成立
(填:成立或不成立).(3)若四边形ABCD是矩形,AB=6,cos∠ACD=
| 3 |
| 5 |
| 1 |
| 2 |
分析:(1)根据①当点E在射线BC边上,且交点P在对角线AC上时,②P、C两点重合时,③当点E在BC边的延长线上且点P在对角线AC的延长线上时,利用三角形的全等判定以及正方形性质,可以得出PE⊥PD,PE=PD;
(2)当四边形ABCD是矩形,无法证明△BAP≌△DAP,故(1)中的猜想不成立.
(3)根据①当点P在线段AC上时,②当点P在线段AC的延长线上时,利用三角形相似得出,分别分析即可得出y与x之间的函数关系式.
(2)当四边形ABCD是矩形,无法证明△BAP≌△DAP,故(1)中的猜想不成立.
(3)根据①当点P在线段AC上时,②当点P在线段AC的延长线上时,利用三角形相似得出,分别分析即可得出y与x之间的函数关系式.
解答: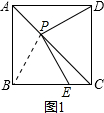 解:(1)PE=PD,PE⊥PD
解:(1)PE=PD,PE⊥PD
①如图1,2,当点E在射线BC边上,且交点P在对角线AC上时,连接PB
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP.
在△BAP与△DAP中,
∵
,
∴△BAP≌△DAP(SAS).
∴PB=PD,
∵点P在BE的垂直平分线上,
∴PB=PE,
∴PE=PD,
∵△BAP≌△DAP,
∴∠DPA=∠APB.
又∵∠APB=180°-45°-∠ABP=135°-∠ABP,
∴∠DPA=135°-∠ABP.
又∵PE=PB,
∴∠BPE=180°-2∠PBE,
∴∠DPE=360°-∠DPA-∠APB-∠BPE,
=360°-2(135°-∠ABP)-180°+2∠PBE,
=360°-270°+2∠ABP-180°+2∠PBE,
=90°,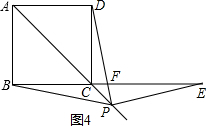
∴PE⊥PD;
②如图3,P、C两点重合,DC=CE,∠DCE=90°,
则PE=PD,PE⊥PD.
③如图4,当点E在BC边的延长线上且点P在对角线AC的延长线上时,
连接PB,
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP.
在△BAP与△DAP中
∵
,
∴△BAP≌△DAP(SAS).
∴PB=PD,
∴∠PBA=∠PDA,
∴∠PBE=∠PDC,
∵点P在BE的垂直平分线上,
∴PB=PE,
∴∠PBE=∠PEB,
∴∠PDC=∠PEB,
∴∠DFC=∠EFP,
∴∠EPF=∠DCF=90°,
∴PE⊥PD,
故结论PE=PD,PE⊥PD 成立;
(2)当四边形ABCD是矩形,无法证明△BAP≌△DAP,
故(1)中的猜想不成立.
故答案为:不成立;
(3)①如图5,当点P在线段AC上时,
∵四边形ABCD是矩形,AB=6,
∴DC=AB=6,
∴∠ABC=∠ADC=90°,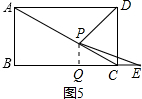
∵cos∠ACD=
=
,
∴AD=8,AC=10,
作PQ⊥BC于点Q,
∴PQ∥AB,
∴
=
,
∴
=
,
∴BQ=
x,
∴BE=
x,
∴CE=
x-8,
∴△CPQ∽△CAB,
∴
=
,
∴
=
,
∴PQ=6-
x,
∴y=
EC×PQ,
=
(
x-8)( 6-
x),
=-
x2+
x-24(5<x<10);
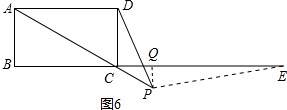
②如图6,当点P在线段AC的延长线上时,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴
=
,
∴
=
,
∴PQ=
x-6,
∴
=
,
∴
=
,
∴CQ=
x-8,
∴BQ=
x,
∴BE=
x,
∴EC=
x-8,
∴y=
EC×PQ,
=
(
x-8)(
x-6),
=
x2-
x+24(x>10).
 解:(1)PE=PD,PE⊥PD
解:(1)PE=PD,PE⊥PD ①如图1,2,当点E在射线BC边上,且交点P在对角线AC上时,连接PB
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP.
在△BAP与△DAP中,
∵
|
∴△BAP≌△DAP(SAS).

∴PB=PD,
∵点P在BE的垂直平分线上,
∴PB=PE,
∴PE=PD,
∵△BAP≌△DAP,
∴∠DPA=∠APB.
又∵∠APB=180°-45°-∠ABP=135°-∠ABP,
∴∠DPA=135°-∠ABP.
又∵PE=PB,
∴∠BPE=180°-2∠PBE,
∴∠DPE=360°-∠DPA-∠APB-∠BPE,
=360°-2(135°-∠ABP)-180°+2∠PBE,
=360°-270°+2∠ABP-180°+2∠PBE,
=90°,

∴PE⊥PD;
②如图3,P、C两点重合,DC=CE,∠DCE=90°,
则PE=PD,PE⊥PD.
③如图4,当点E在BC边的延长线上且点P在对角线AC的延长线上时,
连接PB,
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP.
在△BAP与△DAP中
∵
|
∴△BAP≌△DAP(SAS).
∴PB=PD,
∴∠PBA=∠PDA,
∴∠PBE=∠PDC,
∵点P在BE的垂直平分线上,
∴PB=PE,
∴∠PBE=∠PEB,
∴∠PDC=∠PEB,
∴∠DFC=∠EFP,
∴∠EPF=∠DCF=90°,
∴PE⊥PD,
故结论PE=PD,PE⊥PD 成立;
(2)当四边形ABCD是矩形,无法证明△BAP≌△DAP,
故(1)中的猜想不成立.
故答案为:不成立;
(3)①如图5,当点P在线段AC上时,
∵四边形ABCD是矩形,AB=6,
∴DC=AB=6,
∴∠ABC=∠ADC=90°,

∵cos∠ACD=
| CD |
| AC |
| 3 |
| 5 |
∴AD=8,AC=10,
作PQ⊥BC于点Q,
∴PQ∥AB,
∴
| PC |
| PA |
| CQ |
| BQ |
∴
| 10-x |
| x |
| 8-BQ |
| BQ |
∴BQ=
| 4 |
| 5 |
∴BE=
| 8 |
| 5 |
∴CE=
| 8 |
| 5 |
∴△CPQ∽△CAB,
∴
| PQ |
| AB |
| CP |
| CA |
∴
| PQ |
| 6 |
| 10-x |
| 10 |
∴PQ=6-
| 3 |
| 5 |
∴y=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 8 |
| 5 |
| 3 |
| 5 |
=-
| 12 |
| 25 |
| 36 |
| 5 |
②如图6,当点P在线段AC的延长线上时,
∵PQ∥AB,
∴△CPQ∽△CAB,
∴
| PQ |
| AB |
| PC |
| AC |
∴
| PQ |
| 6 |
| x-10 |
| 10 |

∴PQ=
| 3 |
| 5 |
∴
| PC |
| AC |
| CQ |
| BC |
∴
| x-10 |
| 10 |
| CQ |
| 8 |
∴CQ=
| 4 |
| 5 |
∴BQ=
| 4 |
| 5 |
∴BE=
| 8 |
| 5 |
∴EC=
| 8 |
| 5 |
∴y=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 8 |
| 5 |
| 3 |
| 5 |
=
| 12 |
| 25 |
| 36 |
| 5 |
点评:此题主要考查了正方形的性质以及全等三角形的判定与性质、相似三角形的性质的判定与性质等知识,此题涉及到分类讨论思想,这是数学中常用思想同学们应有意识的应用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
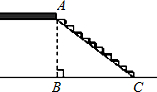 (2012•通州区一模)某地区准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为
(2012•通州区一模)某地区准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为 (2012•通州区一模)如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC,点A在圆内,且AC恰好经过点O,其中BC=12,OA=8,则BD的长为( )
(2012•通州区一模)如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC,点A在圆内,且AC恰好经过点O,其中BC=12,OA=8,则BD的长为( )