题目内容
（2012•通州区一模）如图，BD是⊙O的弦，点C在BD上，以BC为边作等边三角形△ABC，点A在圆内，且AC恰好经过点O，其中BC=12，OA=8，则BD的长为（ ）分析：过O作OE⊥BC于E，由垂径定理求出BD=2BE，求出∠ACB=60°，AC=BC=12，求出OC=4，∠COE=30°，求出CE=2，求出BE，代入BD=2BE即可求出答案．
解答：解：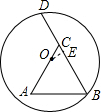
过O作OE⊥BC于E，由垂径定理得：BD=2BE．
∵△ABC是等边三角形，BC=12，
∴∠ACB=60°，AC=BC=12，
∵OA=8，
∴OC=12-8=4，∠COE=30°，
∴CE=
OC=2，
∴BE=12-2=10，
即BD=2BE=20，
故选A．
过O作OE⊥BC于E，由垂径定理得：BD=2BE．∵△ABC是等边三角形，BC=12，
∴∠ACB=60°，AC=BC=12，
∵OA=8，
∴OC=12-8=4，∠COE=30°，
∴CE=
| 1 |
| 2 |
∴BE=12-2=10，
即BD=2BE=20，
故选A．
点评：本题考查了勾股定理，等边三角形性质，垂径定理的应用，题目比较典型，是一道具有一定代表性的题目，通过做此题培养了学生分析问题和解决问题的能力．
练习册系列答案
相关题目
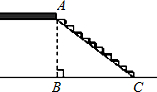（2012•通州区一模）某地区准备修建一座高AB=6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为
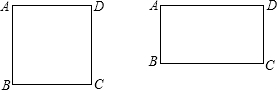（2012•通州区一模）已知四边形ABCD，点E是射线BC上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交射线AC于点P，连接DP，PE．