题目内容
如图1,在平面直角坐标系中,A( ,0),B(0,
,0),B(0, ),且
),且 、
、 满足
满足 .
.
(1)求直线AB的解析式;
(2)若点M为直线 在第一象限上一点,且△ABM是等腰直角三角形,求
在第一象限上一点,且△ABM是等腰直角三角形,求 的值.
的值.
(3)如图3过点A的直线 交
交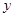 轴负半轴于点P,N点的横坐标为-1,过N点的直线
轴负半轴于点P,N点的横坐标为-1,过N点的直线 交AP于点M,给出两个结论:①
交AP于点M,给出两个结论:① 的值是不变;②
的值是不变;② 的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。
的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。



 ,0),B(0,
,0),B(0, ),且
),且 、
、 满足
满足 .
.(1)求直线AB的解析式;
(2)若点M为直线
 在第一象限上一点,且△ABM是等腰直角三角形,求
在第一象限上一点,且△ABM是等腰直角三角形,求 的值.
的值.(3)如图3过点A的直线
 交
交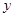 轴负半轴于点P,N点的横坐标为-1,过N点的直线
轴负半轴于点P,N点的横坐标为-1,过N点的直线 交AP于点M,给出两个结论:①
交AP于点M,给出两个结论:① 的值是不变;②
的值是不变;② 的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。
的值是不变,只有一个结论是正确,请你判断出正确的结论,并加以证明和求出其值。


解:(1)由题意求得 A(2,0) B(0,4)
利用待定系数法求得函数解析式为:
(2)分三种情况
当BM⊥BA 且BM=BA时 当AM⊥BA 且AM=BA时 当AM⊥BM 且AM=BM时
△ BMN≌△ABO(AAS) △BOA≌△ANM(AAS)
得M的坐标为(4,6 ) 得M的坐标为(6, 4 ) 构建正方形
m=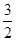 m=
m=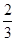 m=1
m=1



(3)结论2是正确的且定值为2
设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,

由 与x轴交于H点可得H(1,0)
与x轴交于H点可得H(1,0)
由 与
与 交于M点可求M(3,K)
交于M点可求M(3,K)
而A(2,0) 所以A为HG的中点
所以△AMG≌△ADH(ASA)
又因为N点的横坐标为-1,且在 上
上
所以可得N 的纵坐标为-K,同理P的纵坐标为-2K
所以ND平行于x轴且N、D的很坐标分别为-1、1
所以N与D关于y轴对称
所以可证△AMG≌△ADH≌△DPC≌△NPC
所以PN=PD=AD=AM
所以 = 2
= 2
利用待定系数法求得函数解析式为:

(2)分三种情况
当BM⊥BA 且BM=BA时 当AM⊥BA 且AM=BA时 当AM⊥BM 且AM=BM时
△ BMN≌△ABO(AAS) △BOA≌△ANM(AAS)
得M的坐标为(4,6 ) 得M的坐标为(6, 4 ) 构建正方形
m=
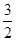 m=
m=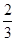 m=1
m=1


(3)结论2是正确的且定值为2
设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,

由
 与x轴交于H点可得H(1,0)
与x轴交于H点可得H(1,0) 由
 与
与 交于M点可求M(3,K)
交于M点可求M(3,K)而A(2,0) 所以A为HG的中点
所以△AMG≌△ADH(ASA)
又因为N点的横坐标为-1,且在
 上
上所以可得N 的纵坐标为-K,同理P的纵坐标为-2K
所以ND平行于x轴且N、D的很坐标分别为-1、1
所以N与D关于y轴对称
所以可证△AMG≌△ADH≌△DPC≌△NPC
所以PN=PD=AD=AM
所以
 = 2
= 2 (1)求出a、b的值得到A、B的坐标,设直线AB的解析式是y=kx+b,代入得到方程组,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥Y轴于N,证△BMN≌△ABO(AAS),求出M的坐标即可;②当AM⊥BA,且AM=BA时,过M作MN⊥X轴于N,同法求出M的坐标;③当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,证△BHM≌△AMN,求出M的坐标即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案
(2)当BM⊥BA,且BM=BA时,过M作MN⊥Y轴于N,证△BMN≌△ABO(AAS),求出M的坐标即可;②当AM⊥BA,且AM=BA时,过M作MN⊥X轴于N,同法求出M的坐标;③当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,证△BHM≌△AMN,求出M的坐标即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 的图象如右图所示,则不等式0≤
的图象如右图所示,则不等式0≤ <5的解集为 .
<5的解集为 .
 。
。 的面积。
的面积。
 (2,4)在正比例函数的图象上,这个正比例函数的解析式是 .
(2,4)在正比例函数的图象上,这个正比例函数的解析式是 . (千克)与月份
(千克)与月份
 的关系如下表所示:
的关系如下表所示: (千克)与月份
(千克)与月份 的函数关系为:
的函数关系为: ;
; (元)与月份
(元)与月份 的函数关系为:
的函数关系为: ;而在6到12月每千克桃脯的价格
;而在6到12月每千克桃脯的价格 (元)与月份
(元)与月份
 ,且其中的
,且其中的 是用于出口,剩余部分由经销点国内销售,每月出口桃脯的售价每千克降低了
是用于出口,剩余部分由经销点国内销售,每月出口桃脯的售价每千克降低了 ,而国内销售的桃脯价格每千克上涨了
,而国内销售的桃脯价格每千克上涨了 ,这样该经销点1到4月销售桃脯的总额为142560元,试求出
,这样该经销点1到4月销售桃脯的总额为142560元,试求出 的值.
的值.  ,
,  ,
,  ,
,  )
) 与y轴的交点坐标是( ).
与y轴的交点坐标是( ). )
)  )
) 的图象不经过第四象限,则
的图象不经过第四象限,则 的取值范围是
的取值范围是

 、
、 在直线
在直线 上,若
上,若 ,则
,则 与
与 大小关系是( )
大小关系是( )

