题目内容
【题目】已知:如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC.BE与DF有怎样的位置关系?为什么?
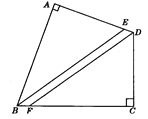
【答案】BE∥DF,理由见解析.
【解析】
根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
本题解析:
BE∥DF,理由:
∵∠A=∠C=90°,
∴∠A+∠C=180°.
∴∠ABC+∠ADC=360°-180°=180°.
∵∠ABE=![]() ∠ABC,∠ADF=
∠ABC,∠ADF=![]() ∠ADC,
∠ADC,
∴∠ABE+∠ADF=![]() (∠ABC+∠ADC)=
(∠ABC+∠ADC)=![]() ×180°=90°.
×180°=90°.
又∵∠ABE+∠AEB=90°,
∴∠AEB=∠ADF,
∴BE∥DF(同位角相等,两直线平行).

 阅读快车系列答案
阅读快车系列答案【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将![]() 地的茶叶1000吨和
地的茶叶1000吨和![]() 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的![]() 地和
地和![]() 地,
地,![]() 地和
地和![]() 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从![]() 、
、![]() 两地运茶叶到
两地运茶叶到![]() 、
、![]() 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设![]() 地运到
地运到![]() 地的茶叶为
地的茶叶为![]() 吨,
吨,
|
| |
| 35 | 40 |
| 30 | 45 |
(1)用含![]() 的代数式填空:
的代数式填空:![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________.
地的茶叶吨数为___________.
(2)用含![]() (吨)的代数式表示总运费
(吨)的代数式表示总运费![]() (元),并直接写出自变量
(元),并直接写出自变量![]() 的取值范围;
的取值范围;
(3)求最低总运费,并说明总运费最低时的运送方案.
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?