题目内容
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
【答案】54°或144°
【解析】分析:分两种情况:①点F在AD上时,可求出∠DEF=81°,在△CDE中可求出∠CED=63°,故可求出∠CEF=144°;②点F在DB上时,可求出∠DEF=9°,故可求出∠CEF=54°.
详解:①点F在AD上时,如图1,
∵AC=BC,D是AB的中点,且∠ACB=90°,
∴∠ADC=90°,∠DCE=45°
∵∠CDE=72°
∴∠EDF=18°
∵DE=DF
∴∠DEF=81°
在△ECD中,∠CDE=72°,∠ECD=45°
∴∠CED=63°,
∴∠CEF=144°;
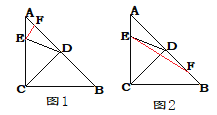
②点F在DB上时,如图2.
同理得,∠DEF=9°,
∴∠CEF=54°.
故答案为:54°或144°.

练习册系列答案
相关题目