题目内容
【题目】我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费;即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
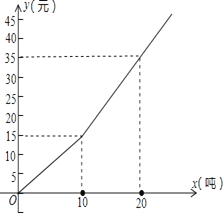
(1)分段写出y与x的函数关系式.
(2)某户居民上月用水8吨,应收水费多少元?
(3)已知居民甲上月比居民乙多用水4吨,两家一共交水费46元,求他们上月分别用水多少吨?
【答案】(1)x≤10,y=1.5x;x>10,y=2x-5;(2)12元;(3)甲16吨,乙12吨
【解析】
试题(1)当x≤10时,设函数关系式为![]() ,根据图象过点(10,15)即可根据待定系数法求得函数关系式,当x>10时,设函数关系式为
,根据图象过点(10,15)即可根据待定系数法求得函数关系式,当x>10时,设函数关系式为![]() ,根据图象过点(10,15)、(20,35)即可根据待定系数法求得函数关系式;
,根据图象过点(10,15)、(20,35)即可根据待定系数法求得函数关系式;
(2)把![]() 代入对应的函数关系式即可求得结果;
代入对应的函数关系式即可求得结果;
(3)先判断出两家水费量的范围,再设甲、乙两户上月用水分别为m、n吨,根据居民甲上月比居民乙多用水4吨,两家一共交水费46元,即可列方程组求解.
(1)当x≤10时,设函数关系式为![]() ,
,
∵图象过点(10,15)
∴![]() ,
,![]()
∴当x≤10时,函数关系式为![]()
当x>10时,设函数关系式为![]() ,
,
∵图象过点(10,15)、(20,35)
∴![]() ,解得
,解得![]()
∴当x>10时,函数关系式为![]() ;
;
(2)当x=8时,y=8×1.5=12元,
答:用水8吨,应收水费12元;
(3)∵1.5×10+1.5×10+2×4<46
∴两家用水均超过10吨
设甲、乙两户上月用水分别为m、n吨,由题意得
![]()
解得![]()
答:甲用水16吨,乙用水12吨.

 走进文言文系列答案
走进文言文系列答案【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?