题目内容
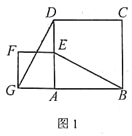
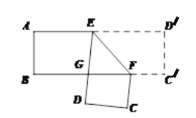
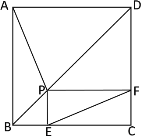
【题目】如图,在平行四边形ABCD中,点E是CD的中点,点F是BC边上的点,AF=AD+FC,平行四边形ABCD的面积为S,由A、E、F三点确定的圆的周长为t.
(1)若△ABE的面积为30,直接写出S的值;
(2)求证:AE平分∠DAF;
(3)若AE=BE,AB=4,AD=5,求t的值.
【答案】(1)平行四边形ABCD的面积为60;(2)证明见解析;(3)△AEF的外接圆的周长t=![]() π.
π.
【解析】(1)作EG⊥AB于点G,由S△ABE=![]() ×AB×EG=30得ABEG=60,即可得出答案;
×AB×EG=30得ABEG=60,即可得出答案;
(2)延长AE交BC延长线于点H,先证△ADE≌△HCE得AD=HC、AE=HE及AD+FC=HC+FC,结合AF=AD+FC得∠FAE=∠CHE,根据∠DAE=∠CHE即可得证;
(3)先证∠ABF=90°,根据勾股定理可得出AF2=AB2+BF2=16+(5﹣FC)2=(FC+CH)2=(FC+5)2,据此求得FC的长,从而得出AF的长度,再由AE=HE、AF=FH知FE⊥AH,即AF是△AEF的外接圆直径,从而得出答案.
(1)如图,作EG⊥AB于点G,
则S△ABE=![]() ×AB×EG=30,则ABEG=60,
×AB×EG=30,则ABEG=60,
∴平行四边形ABCD的面积为60;
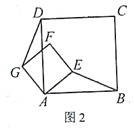
(2)如图,延长AE交BC延长线于点H,

∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠HCE,∠DAE=∠CHE,
∵E为CD的中点,
∴CE=ED,
∴△ADE≌△HCE,
∴AD=HC、AE=HE,
∴AD+FC=HC+FC,
由AF=AD+FC和FH=HC+FC得AF=FH,
∴∠FAE=∠CHE,
又∵∠DAE=∠CHE,
∴∠DAE=∠FAE,
∴AE平分∠DAF;
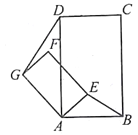
(3)连接EF,
∵AE=BE、AE=HE,
∴AE=BE=HE,
∴∠BAE=∠ABE,∠HBE=∠BHE,
∵∠DAE=∠CHE,
∴∠BAE+∠DAE=∠ABE+∠HBE,即∠DAB=∠CBA,
由四边形ABCD是平行四边形得∠DAB+∠CBA=180°,
∴∠CBA=90°,
∴AF2=AB2+BF2=16+(5﹣FC)2=(FC+CH)2=(FC+5)2,
解得:FC=![]() ,
,
∴AF=FC+CH=![]() ,
,
∵AE=HE、AF=FH,
∴FE⊥AH,
∴AF是△AEF的外接圆直径,
∴△AEF的外接圆的周长t=![]() π.
π.

【题目】油电混动汽车是一种节油、环保的新技术汽车.它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中.汽车在低速行驶时,使用蓄电池带动电动机驱动汽车,节约燃油.某品牌油电混动汽车与普通汽车的相关成本数据估算如下:
油电混动汽车 | 普通汽车 | |
购买价格(万元) | 17.48 | 15.98 |
每百公里燃油成本(元) | 31 | 46 |
某人计划购入一辆上述品牌的汽车.他估算了用车成本,在只考虑车价和燃油成本的情况下,发现选择油电混动汽车的成本不高于选择普通汽车的成本.则他在估算时,预计行驶的公里数至少为多少公里?