题目内容
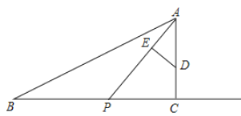
【题目】△ABC中,点O是AC上一动点,过点O作直线MN∥BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.
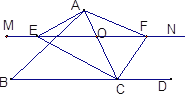
⑴说明:OE=OF
⑵当点O运动到何处时,四边形AECF是矩形,证明你的结论
⑶在⑵的条件下,当⊿ABC满足什么条件时,四边形AECF为正方形.
【答案】(1)证明见解析;(2)当点O运动到AC的中点时,证明见解析;(3)△ABC满足∠ACB为直角的直角三角形时,证明见解析.
【解析】
(1)利用平行线的特殊性质,内错角相等,以及角平分线的性质,等量代换,最后求出![]() ;
;
(2)先证明平行四边形,再证明对角线相等,推出四边形为矩形;
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
(1)∵MN∥BC,
∴![]() ,
,![]() ,
,
又已知CE平分∠BCO,CF平分∠DCO,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,![]() ,
,
又∵![]() ,
,
∴四边形AECF是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴四边形AECF是矩形;
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当![]() ,则
,则
![]() ,
,
∴AC⊥EF,
∴四边形AECF是正方形.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.