题目内容
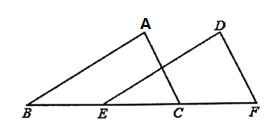
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 从
从![]() 点出发沿射线
点出发沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度向右运动.设点
个单位的速度向右运动.设点![]() 的运动时间为
的运动时间为![]() .连结
.连结![]() .
.
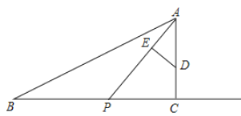
(1)当![]() 秒时,求
秒时,求![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值;
的值;
(3)过点![]() 做
做![]() 于点
于点![]() .在点
.在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,能使
为何值时,能使![]() ?
?
【答案】(1)2![]() ;(2)4
;(2)4![]() 或16或5;(3)5或11.
或16或5;(3)5或11.
【解析】
(1)根据题意得BP=2t,从而求出PC的长,然后利用勾股定理即可求出AP的长;
(2)先利用勾股定理求出AB的长,然后根据等腰三角形腰的情况分类讨论,分别列出方程即可求出t的值;
(3)根据点P的位置分类讨论,分别画出对应的图形,根据勾股定理求出AE,分别利用角平分线的性质和判定求出AP,利用勾股定理列出方程,即可求出t的值.
(1)根据题意,得BP=2t,
∴PC=16-2t=16-2×3=10,
∵AC=8,
在Rt△APC中,根据勾股定理,得AP=![]() =
=![]() =2
=2![]() .
.
答:AP的长为2![]() .
.
(2)在Rt△ABC中,AC=8,BC=16,
根据勾股定理,得AB=![]() =
=![]() =8
=8![]()
若BA=BP,
则 2t=8![]() ,
,
解得:t=4![]() ;
;
若AB=AP,
∴此时AC垂直平分BP
则BP=32,
2t=32,
解得:t=16;
若PA=PB=2t,CP=16-2t
∵PA2= CP2+AC2
则(2t)2=(16-2t)2+82,
解得:t=5.
答:当△ABP为等腰三角形时,t的值为4![]() 、16、5.
、16、5.
(3)若P在C点的左侧,连接PD
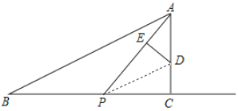
CP=16-2t
∵DE=DC=3,AC=8,![]() ,DC⊥PC
,DC⊥PC
∴PD平分∠EPC,AD=AC-DC=5
根据勾股定理可得AE=![]() ,
,
∴∠EPD=∠CPD
∴∠EDP=90°-∠EPD=90°-∠CPD=∠CDP
∴DP平分∠EDC
∴PE=CP=162t
∴AP=AE+EP=20-2t
∵PA2= CP2+AC2
则(20-2t)2=(16-2t)2+82,
解得:t=5;
若P在C点的右侧,连接PD
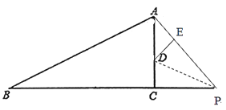
CP=2t-16
∵DE=DC=3,AC=8,![]() ,DC⊥PC
,DC⊥PC
∴PD平分∠EPC,AD=AC-DC=5
根据勾股定理可得AE=![]()
∴∠EPD=∠CPD
∴∠EDP=90°-∠EPD=90°-∠CPD=∠CDP
∴DP平分∠EDC
∴PE=CP=2t-16
∴AP=AE+EP=2t-12
∵PA2= CP2+AC2
则(2t-12)2=(2t-16)2+82,
解得:t=11;
答:当t为5或11时,能使DE=CD.