题目内容
已知:在Rt△ABC中,∠C=90°,D是AB上一点.过点D作一直线截原三角形形成小三角形,并使它和原三角形相似.如果AB=10,AC:BC=3:4,AD=6.请求出DE的长.(注:点E是过点D的直线与△ABC另一边的交点)分析:由题意,这样的小三角形可以作出三个,如下图所示,利用相似三角形的对应边成比例,逐个计算即可.
解答: 解:依题意得:AB=10,AC=6,BC=8,BD=4,这样的小三角形可以作出三个.
解:依题意得:AB=10,AC=6,BC=8,BD=4,这样的小三角形可以作出三个.
情况1:过点D作DE∥AC,交BC于点E,
∴∠BDE=∠A,
∵∠B=∠B,
∴△BDE∽△BAC.
∴
=
.
∴DE=
•AC=
×6=2.4.
情况2:过点D作DE∥BC,交AC于点E,
∴∠ADE=∠B,
∵∠A=∠A
∴△ADE∽△ABC
∴
=
.
∴DE=
•BC=
×8=4.8.
情况3:过点D作DE⊥AB交BC于点E,
∴∠BDE=90°,
∵∠C=90°
∴∠BDE=∠C,∠B=∠B,
∴△BDE∽△BCA
∴
=
.∴DE=
•AC=
×6=3.
 解:依题意得:AB=10,AC=6,BC=8,BD=4,这样的小三角形可以作出三个.
解:依题意得:AB=10,AC=6,BC=8,BD=4,这样的小三角形可以作出三个.情况1:过点D作DE∥AC,交BC于点E,
∴∠BDE=∠A,
∵∠B=∠B,
∴△BDE∽△BAC.
∴
| DE |
| AC |
| BD |
| BA |
∴DE=
| BD |
| BA |
| 4 |
| 10 |
情况2:过点D作DE∥BC,交AC于点E,
∴∠ADE=∠B,
∵∠A=∠A
∴△ADE∽△ABC
∴
| DE |
| BC |
| AD |
| AB |
∴DE=
| AD |
| AB |
| 6 |
| 10 |
情况3:过点D作DE⊥AB交BC于点E,
∴∠BDE=90°,
∵∠C=90°
∴∠BDE=∠C,∠B=∠B,
∴△BDE∽△BCA
∴
| DE |
| AC |
| BD |
| BC |
| BD |
| BC |
| 4 |
| 8 |
点评:本题考查相似三角形的判定和性质,属开放型的题目,难度不大,但是容易漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
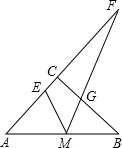 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.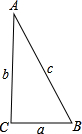 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=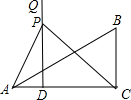 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.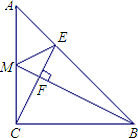 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB. 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.