题目内容
 已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.(1)观察图形,猜想BD与⊙O的位置关系:
相切
相切
;(2)证明第(1)题的猜想.
分析:(1)观察图形,可得BD与⊙O的位置关系:相切;
(2)首先连接OD,由AE是⊙O的直径,在Rt△ABC中,∠C=90°,易证得DE∥BC,又由∠CBD=∠A,可证得∠ODE+∠EDB=90°,即可证得结论.
(2)首先连接OD,由AE是⊙O的直径,在Rt△ABC中,∠C=90°,易证得DE∥BC,又由∠CBD=∠A,可证得∠ODE+∠EDB=90°,即可证得结论.
解答: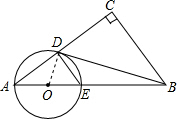 (1)解:相切.
(1)解:相切.
故答案为:相切.
(2)证明:连接OD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠A+∠AED=90°,
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
∴∠EDB=∠CBD,
∵∠CBD=∠A,
∴∠EDB=∠A,
∵OD=OE,
∴∠ODE=∠OED,
∴∠ODE+∠EDB=90°,
即OD⊥BD,
∴BD与⊙O的位置关系是相切.
 (1)解:相切.
(1)解:相切.故答案为:相切.
(2)证明:连接OD,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠A+∠AED=90°,
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
∴∠EDB=∠CBD,
∵∠CBD=∠A,
∴∠EDB=∠A,
∵OD=OE,
∴∠ODE=∠OED,
∴∠ODE+∠EDB=90°,
即OD⊥BD,
∴BD与⊙O的位置关系是相切.
点评:此题考查了切线的判定以及平行线的判定与性质.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
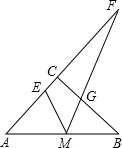 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.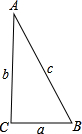 已知:在Rt△ABC中,∠C=90°,∠A=30°,b=
已知:在Rt△ABC中,∠C=90°,∠A=30°,b=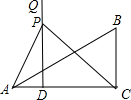 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.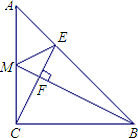 已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.
已知:在Rt△ABC中,∠C=90°,AC=BC,M是AC的中点,连接BM,CF⊥MB,F是垂足,延长CF交AB于点E.求证:∠AME=∠CMB.