题目内容
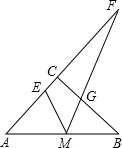 如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.
如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,M是边AB的中点,E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F.(1)在不添加字母和线段的情况下写出图中一定相似的三角形,并证明其中的一对;
(2)连接结EG,当AE=3时,求EG的长.
分析:(1)因为△ABC是等腰直角三角形,从而可得到∠A=∠B=45°,再根据外角的性质得到∠AEM=∠BMG,从而可根据有两组角相等的两个三角形相似,得到△AEM∽△BMG,同理可证明△FEM∽△FMA.
(2)根据勾股定理可求得AB的长,从而可得到AM,BM的长,再根据相似三角形的判定及性质,根据相似比即可求得EG的长.
(2)根据勾股定理可求得AB的长,从而可得到AM,BM的长,再根据相似三角形的判定及性质,根据相似比即可求得EG的长.
解答: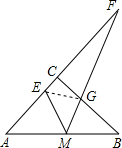 解:(1)一定相似的三角形:△AEM∽△BMG,△FEM∽△FMA,(2分)
解:(1)一定相似的三角形:△AEM∽△BMG,△FEM∽△FMA,(2分)
以下证明△AEM∽△BMG
∵Rt△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°.(1分)
∵∠EMB=∠EMG+∠GMB=∠A+∠AEM,
∵∠EMG=45°,
∴∠AEM=∠BMG.(1分)
∴△AEM∽△BMG.(2分)
(2)∵在Rt△ABC中,∠ACB=90°,AC=BC=4,
∴AB=
=4
.(1分)
∵M为AB的中点,
∴AM=BM=2
.
∵△AME∽△BGM,
∴
=
∴
=
.
∴BG=
.(2分)
∴CG=4-
=
,CE=4-3=1.(2分)
∴EG=
=
.(1分)
 解:(1)一定相似的三角形:△AEM∽△BMG,△FEM∽△FMA,(2分)
解:(1)一定相似的三角形:△AEM∽△BMG,△FEM∽△FMA,(2分)以下证明△AEM∽△BMG
∵Rt△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°.(1分)
∵∠EMB=∠EMG+∠GMB=∠A+∠AEM,
∵∠EMG=45°,
∴∠AEM=∠BMG.(1分)
∴△AEM∽△BMG.(2分)
(2)∵在Rt△ABC中,∠ACB=90°,AC=BC=4,
∴AB=
| AC2+BC2 |
| 2 |
∵M为AB的中点,
∴AM=BM=2
| 2 |
∵△AME∽△BGM,
∴
| AE |
| BM |
| AM |
| BG |
| 3 | ||
2
|
2
| ||
| BG |
∴BG=
| 8 |
| 3 |
∴CG=4-
| 8 |
| 3 |
| 4 |
| 3 |
∴EG=
| CE2+CG2 |
| 5 |
| 3 |
点评:此题主要考查学生对相似三角形的判定及性质和勾股定理等知识点的掌握情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
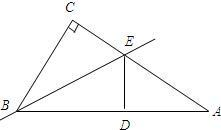 如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.
如图,已知,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合.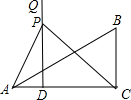 重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.
重合),过D作DQ⊥AC(DQ与AB在AC的同侧);点P从D点出发,在射线DQ上运动,连接PA、PC.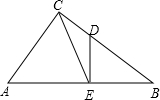 如图,已知:在Rt△ABC中,∠ACB=90°,sinB=
如图,已知:在Rt△ABC中,∠ACB=90°,sinB= 21、如图,已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=3,AM=AC,BN=BC.
21、如图,已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=3,AM=AC,BN=BC. 如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.
如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.