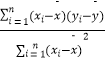题目内容
【题目】已知圆：（x+cosθ）2+（y﹣sinθ）2=1，直线l：y=kx．给出下面四个命题： ①对任意实数k和θ，直线l和圆M有公共点；
②对任意实数k，必存在实数θ，使得直线l和圆M相切；
③对任意实数θ，必存在实数k，使得直线l和圆M相切；
④存在实数k和θ，使得圆M上有一点到直线l的距离为3．
其中正确的命题是（写出所以正确命题的编号）
【答案】①②
【解析】解：∵圆：（x+cosθ）2+（y﹣sinθ）2=1恒过定点O（0，0） 直线l：y=kx也恒过定点O（0，0），
∴①正确；
圆心M（﹣cosθ，sinθ）
圆心到直线的距离d= 
= 
≤1，
∴对任意实数k和θ，直线l和圆M的关系是相交或者相切，
∴②正确，③④都错误．
所以答案是：①②．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某同学在研究性学习中，收集到某制药厂今年前5个月甲胶囊生产产量（单位：万盒）的数据如下表所示：
月份x | 1 | 2 | 3 | 4 | 5 |
y（万盒） | 4 | 4 | 5 | 6 | 6 |
（1）该同学为了求出y关于x的线性回归方程 
= 
+ 
，根据表中数据已经正确计算出 
=0.6，试求出 的值，并估计该厂6月份生产的甲胶囊产量数；
（2）若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒，小红同学从中随机购买了3盒甲胶囊，后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题．记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ，求ξ的分布列和数学期望．
