题目内容
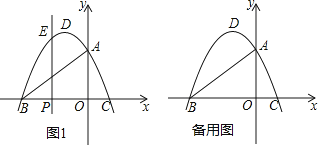
【题目】如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)若CD=![]() ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
【答案】
(1)
解:CD⊥AB,
∴PC=PD=![]() CD=
CD=![]() ,
,
如图,连接OC,
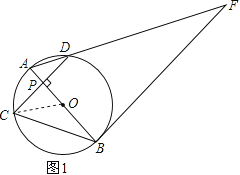
设⊙O的半径为r,则PO=PB﹣r=4﹣r,
在RT△POC中,OC2=OP2+PC2,
即r2=(4﹣r)2+(![]() )2,解得r=
)2,解得r=![]() .
.
(2)
证明:∵∠A=∠C,∠F=∠ABC,
∴∠ABF=∠CPB,
∵CD⊥AB,
∴∠ABF=∠CPB=90°,
∴直线BF是⊙O的切线;
(3)
解:四边形AEBF是平行四边形;
理由:如图2所示:
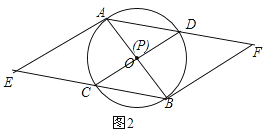
∵CD⊥AB,垂足为P,
∴当点P与点O重合时,CD=AB,
∴OC=OD,
∵AE是⊙O的切线,
∴BA⊥AE,
∵CD⊥AB,
∴DC∥AE,
∵AO=OB,
∴OC是△ABE的中位线,
∴AE=2OC,
∵∠D=∠ABC,∠F=∠ABC.
∴∠D=∠F,
∴CD∥BF,
∵AE∥BF,
∵OA=OB,
∴OD是△ABF的中位线,
∴BF=2OD,
∴AE=BF,
∴四边形AEBF是平行四边形.
【解析】(1)根据垂径定理求得PC,连接OC,根据勾股定理求得即可;
(2)求得△PBC∽△BFA,根据相似三角形对应角相等求得∠ABF=∠CPB=90°,即可证得结论;
(3)通过证得AE=BF,AE∥BF,从而证得四边形AEBF是平行四边形.
此题考查了圆的综合应用,涉及知识点有垂径定理,勾股定理,相似三角形性质和平行四边形判定.

【题目】某商场试销一种商品,成本为每件200元,规定试销期间销售单价不低于成本单价,且获利不得高于50%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
销售量y(件) | … | 440 | 430 | 420 | 410 | … |
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?