题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.
与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D.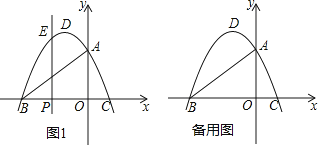
(1)填空:点A的坐标为( , ),点B的坐标为( , ),点C的坐标为( , ),点D的坐标为( , );
(2)点P是线段BC上的动点(点P不与点B、C重合)
①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标;
②在①的条件下,点F是坐标轴上的点,且点F到EA和ED的距离相等,请直接写出线段EF的长;
③若点Q是线段AB上的动点(点Q不与点A、B重合),点R是线段AC上的动点(点R不与点A、C重合),请直接写出△PQR周长的最小值.
【答案】
(1)
解:令x=0,则y=2,
∴A(0,2),
令y=0,则﹣![]() x2﹣
x2﹣![]() x+2=0,解得x1=﹣3,x2=1(舍去),
x+2=0,解得x1=﹣3,x2=1(舍去),
∴B(﹣3,0),C(1,0),
由y=﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+1)2+
(x+1)2+![]() 可知D(﹣1,
可知D(﹣1,![]() ),
),
故答案为:0、2,﹣3、0,1、0,﹣1、![]() ;
;
(2)
解:①设P(n,0),则E(n,﹣![]() n2﹣
n2﹣![]() n+2),
n+2),
∵PE=PC,
∴﹣![]() n2﹣
n2﹣![]() n+2=1﹣n,解得n1=﹣
n+2=1﹣n,解得n1=﹣![]() ,n2=1(舍去),
,n2=1(舍去),
∴当n=﹣![]() 时,1﹣n=
时,1﹣n=![]() ,
,
∴E(﹣![]() ,
,![]() ),
),
②如图1,设直线DE与x轴交于M,与y轴交于N,直线EA与x轴交于K,
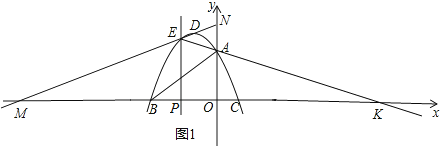
根据E、D的坐标求得直线ED的斜率为![]() ,根据E、A的坐标求得直线EA的斜率为﹣
,根据E、A的坐标求得直线EA的斜率为﹣![]() ,
,
∴△MEK是以MK为底边的等腰三角形,△AEN是以AN为底边的等腰三角形,
∵到EA和ED的距离相等的点F在顶角的平分线上,
根据等腰三角形的性质可知,EF是E点到坐标轴的距离,
∴EF=![]() 或
或![]() ;
;
③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,
如图2,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,
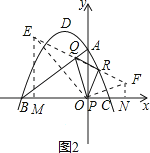
此时△PQR的周长PQ+QR+PR=EF,
∵A(0,2),B(﹣3,0),C(1,0),
∴AB=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ,
,
∵S△AOB=![]() ×
×![]() OE×AB=
OE×AB=![]() OAOB,
OAOB,
∴OE=![]() ,
,
∵△OEM∽△ABO,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴OM=![]() ,EM=
,EM=![]()
∴E(﹣![]() ,
,![]() ),
),
同理求得F(![]() ,
,![]() ),
),
即△PQR周长的最小值为EF=![]() =
=![]() .
.
【解析】(1)令x=0,求得A(0,2),令y=0,求得B(﹣3,0),C(1,0),由y=﹣![]() x2﹣
x2﹣![]() x+2转化成顶点式可知D(﹣1,
x+2转化成顶点式可知D(﹣1,![]() );
);
(2)①设P(n,0),则E(n,﹣![]() n2﹣
n2﹣![]() n+2),根据已知条件得出﹣
n+2),根据已知条件得出﹣![]() n2﹣
n2﹣![]() n+2=1﹣n,解方程即可求得E的坐标;
n+2=1﹣n,解方程即可求得E的坐标;
②根据直线ED和EA的斜率可知直线与坐标轴的交角相等,从而求得与坐标轴构成的三角形是等腰三角形,根据等腰三角形的性质即可求得EF的长;
③根据题意得:当△PQR为△ABC垂足三角形时,周长最小,所以P与O重合时,周长最小,作O关于AB的对称点E,作O关于AC的对称点F,连接EF交AB于Q,交AC于R,此时△PQR的周长PQ+QR+PR=EF,然后求得E、F的坐标,根据勾股定理即可求得.

【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写下表:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 |
| 300 |
| … |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?