题目内容
【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A. B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP![]() ,我们就把∠APB叫做∠MON的关联角.
,我们就把∠APB叫做∠MON的关联角.
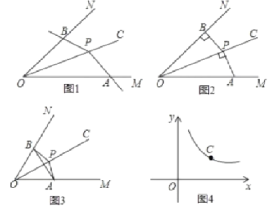
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB___∠MON的关联角(填“是”或“不是”).
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积。
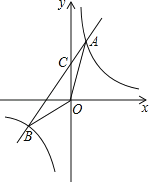
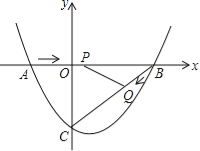
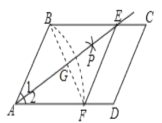
(3)如图4,点C是函数y=![]() (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标。
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标。
【答案】(1) 是;(2)①![]() ,150°;②
,150°;②![]() m×sinα;(3) 点(
m×sinα;(3) 点(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ).
).
【解析】
(1)先判断出△OBP∽△OPA,即可;
(2)①先根据关联角求出OA×OB=4,再利用三角形的面积公式,以及相似,得到∠OAP=∠OPB,即可;②根据三角形面积公式把α和m代入即可;
(3)根据条件分情况讨论,点B在y轴正半轴和负半轴,在负半轴时,经过计算,不存在,②在正半轴时,由BC=2AC判断出点C是线段AB的一个三等分点,即可.
(1)∵P为∠MON平分线OC上一点,
∴∠BOP=∠AOP,
∵PB⊥ON于B,AP⊥OC于P,
∴∠OBP=∠OPA,
∴△OBP∽△OPA,
∴![]() ,
,
∴OP![]() =OA×OB,
=OA×OB,
∴∠APB是∠MON的关联角.
故答案为是.
(2)①如图,过点A作AH⊥OB,
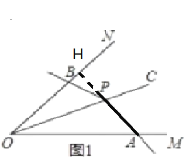
∵∠APB是∠MON的关联角,OP=2,
∴OA×OB=OP![]() =4,
=4,
在Rt△AOH中,∠AOH=90°,
∴sin∠AOH=![]() ,
,
∴AH=OAsin∠AOH,
∴S![]() =
=![]() OB×AH=
OB×AH=![]() OB×OA×sin60°=
OB×OA×sin60°=![]() ×OP
×OP×
![]() =
=![]() ,
,
∵OP![]() =OA×OB,
=OA×OB,
∴![]() ,
,
∵点P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() ∠MON=30°,
∠MON=30°,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°30°=150°,
②由①有,S![]() =
=![]() OB×OA×∠MON=
OB×OA×∠MON=![]() m×sinα;
m×sinα;
(3)∵过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,
∴只有点A在x轴正半轴,
①当点B在y轴负半轴时,设A(m,0),B(0,n)(m>0,n<0)
∴OA=m,OB=n,
∵BC=2CA,
∴点A是BC中点,
∴点C(2m,n),
∵点C在双曲线y=2x上,
∴2m×(n)=2,
∴mn=1(不符合题意,舍去),
∵∠AOB的关联角∠APB
∴OP![]() =OA×0B=|m||n|=1,
=OA×0B=|m||n|=1,
∴OP=1,
∵点P在∠AOB的平分线上,设P(a,a),
∴OP![]() =2a
=2a![]() ,
,
∴2a![]() =1,
=1,
∴a=±![]() ,
,
∴点P(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
②当点B在y轴正半轴,设A(m,0),B(0,n)(m>0,n>0)
∴点C(![]() ),
),
∴=2,
∴mn=9,
∵∠AOB的关联角∠APB
∴OP![]() =OA×0B=mn=9,
=OA×0B=mn=9,
∴OP=3,
∵点P在∠AOB的平分线上,设P(a,a),
∴OP![]() =2a
=2a![]() ,
,
∴2a![]() =9,
=9,
∴a=±![]() ,
,
即:点P![]() (
(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),
),
综上所述,点(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ).
).