Question

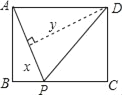
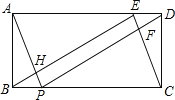
【题目】如图，矩形ABCD中，AB＝2，BC＝5，E、P分别在AD、BC上，且DE＝BP＝1.

(1) 判断△BEC的形状，并说明理由;

(2) 求证：四边形EFPH是矩形.

Answer 1

【答案】（1）△BEC是直角三角形.证明见解析；（2）见解析。

【解析】

(1)根据矩形性质得出CD=2，根据勾股定理求出CE和BE，求出CE2+BE2的值，求出BC2，根据勾股定理的逆定理求出即可；

(2)根据矩形的性质和平行四边形的判定，推出平行四边形DEBP和AECP，推出EH∥FP，EF∥HP，推出平行四边形EFPH，根据矩形的判定推出即可．

(1)△BEC是直角三角形，理由如下：

∵矩形ABCD，

∴∠ADC=∠ABP=90°，

∵AD=BC=5，AB=CD=2，

∴CE==，

同理BE=2，

∴CE2+BE2=5+20=25，

∵BC2=52=25，

∴BE2+CE2=BC2，

∴∠BEC=90°，

∴△BEC是直角三角形；

(2)∵矩形ABCD，

∴AD=BC，AD∥BC，

∵DE=BP，

∴四边形DEBP是平行四边形，

∴BE∥DP，

∵AD=BC，AD∥BC，DE=BP，

∴AE=CP，

∴四边形AECP是平行四边形，

∴AP∥CE，

∴四边形EFPH是平行四边形，

∵∠BEC=90°，

∴平行四边形EFPH是矩形．